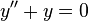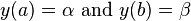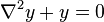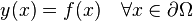Dirichlet boundary condition
In mathematics, the Dirichlet (or first-type) boundary condition is a type of boundary condition, named after Peter Gustav Lejeune Dirichlet (1805–1859).[1] When imposed on an ordinary or a partial differential equation, it specifies the values that a solution needs to take on along the boundary of the domain.
The question of finding solutions to such equations is known as the Dirichlet problem. In engineering applications, a Dirichlet boundary condition may also be referred to as a fixed boundary condition.
Examples
ODE
For an ordinary differential equation, for instance:
the Dirichlet boundary conditions on the interval ![[a, \, b]](../I/m/d2524b9940ce1c636bfb26ae09a941d2.png)
take the form:
where 
and 
are given numbers.
PDE
For a partial differential equation, for instance:
where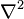 
denotes the Laplacian, the Dirichlet boundary conditions on a domain 
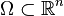take the form:
where f is a known function defined on the boundary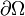 
.
Engineering applications
For example, the following would be considered Dirichlet boundary conditions:
- In mechanical engineering (beam theory), where one end of a beam is held at a fixed position in space.
- In thermodynamics, where a surface is held at a fixed temperature.
- In electrostatics, where a node of a circuit is held at a fixed voltage.
- In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.
Other boundary conditions
Many other boundary conditions are possible, including the Cauchy boundary condition and the mixed boundary condition. The latter is a combination of the Dirichlet and Neumann conditions.
See also
- Neumann boundary condition
- Mixed boundary condition
- Robin boundary condition
- Cauchy boundary condition
- Different types of boundary conditions in fluid dynamics
References
- ↑ Cheng, A. and D. T. Cheng (2005). Heritage and early history of the boundary element method, Engineering Analysis with Boundary Elements, 29, 268–302.