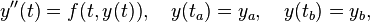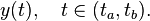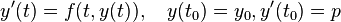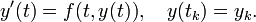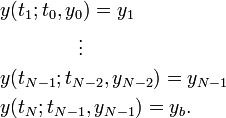Direct multiple shooting method

In the area of mathematics known as numerical ordinary differential equations, the direct multiple shooting method is a numerical method for the solution of boundary value problems. The method divides the interval over which a solution is sought into several smaller intervals, solves an initial value problem in each of the smaller intervals, and imposes additional matching conditions to form a solution on the whole interval. The method constitutes a significant improvement in distribution of nonlinearity and numerical stability over single shooting methods.

Single shooting methods

Shooting methods can be used to solve boundary value problems (BVP) like

y''(t) = f(t, y(t)), \quad y(t_a) = y_a, \quad y(t_b) = y_b,

in which the time points t_a and t_b are known and we seek

y(t),\quad t \in (t_a,t_b).

Single shooting methods proceed as follows. Let y(t; t₀, y₀) denote the solution of the initial value problem (IVP)

y'(t) = f(t, y(t)), \quad y(t_0) = y_0, y'(t_0) = p

Define the function F(p) as the difference between y(t_b; p) and the specified boundary value y_b: F(p) = y(t_b; p) − y_b. Then for every solution (y_a, y_b) of the boundary value problem we have y_a=y₀ while y_b corresponds to a root of F. This root can be solved by any root-finding method given that certain method-dependent prerequisites are satisfied. This often will require initial guesses to y_a and y_b. Typically, analytic root finding is impossible and iterative methods such as Newton's method are used for this task.

The application of single shooting for the numerical solution of boundary value problems suffers from several drawbacks.

For a given initial value y₀ the solution of the IVP obviously must exist on the interval [t_a,t_b] so that we can evaluate the function F whose root is sought.

For highly nonlinear or unstable ODEs, this requires the initial guess y₀ to be extremely close to an actual but unknown solution y_a. Initial values that are chosen slightly off the true solution may lead to singularities or breakdown of the ODE solver method. Choosing such solutions is inevitable in an iterative root-finding method, however.

Finite precision numerics may make it impossible at all to find initial values that allow for the solution of the ODE on the whole time interval.
The nonlinearity of the ODE effectively becomes a nonlinearity of F, and requires a root-finding technique capable of solving nonlinear systems. Such methods typically converge slower as nonlinearities become more severe. The boundary value problem solver's performance suffers from this.
Even stable and well-conditioned ODEs may make for unstable and ill-conditioned BVPs. A slight alteration of the initial value guess y₀ may generate an extremely large step in the ODEs solution y(t_b; t_a, y₀) and thus in the values of the function F whose root is sought. Non-analytic root-finding methods can seldom cope with this behaviour.

Multiple shooting

A direct multiple shooting method partitions the interval [t_a, t_b] by introducing additional grid points

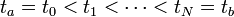t_a = t_0 < t_1 < \cdots < t_N = t_b

The method starts by guessing somehow the values of y at all grid points t_k with 0 ≤ k ≤ N − 1. Denote these guesses by y_k. Let y(t; t_k, y_k) denote the solution emanating from the kth grid point, that is, the solution of the initial value problem

y'(t) = f(t, y(t)), \quad y(t_k) = y_k.

All these solutions can be pieced together to form a continuous trajectory if the values y match at the grid points. Thus, solutions of the boundary value problem correspond to solutions of the following system of N equations:

\begin{align} & y(t_1; t_0, y_0) = y_1 \\ & \qquad\qquad\vdots \\ & y(t_{N-1}; t_{N-2}, y_{N-2}) = y_{N-1} \\ & y(t_N; t_{N-1}, y_{N-1}) = y_b. \end{align}

The central N−2 equations are the matching conditions, and the first and last equations are the conditions y(t_a) = y_a and y(t_b) = y_b from the boundary value problem. The multiple shooting method solves the boundary value problem by solving this system of equations. Typically, a modification of the Newton's method is used for the latter task.

References

Stoer, Josef; Bulirsch, Roland (2002), Introduction to Numerical Analysis (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-95452-3 . See Sections 7.3.5 and further.
Bock, Hans Georg; Plitt, Karl J. (1984), "A multiple shooting algorithm for direct solution of optimal control problems", Proceedings of the 9th IFAC World Congress, Budapest

Morrison, David D.; Riley, James D.; Zancanaro, John F. (December 1962), "Multiple shooting method for two-point boundary value problems", Commun. ACM (New York, NY, USA: ACM) 5 (12): 613–614, doi:10.1145/355580.369128