Direct image with compact support

In mathematics, in the theory of sheaves the direct image with compact (or proper) support is an image functor for sheaves.

Definition

Image functors for sheaves
direct image f_∗
inverse image f^∗
direct image with compact support f_!
exceptional inverse image Rf^!
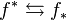$f^* \leftrightarrows f_*$
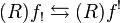$(R)f_! \leftrightarrows (R)f^!$

Let f: X → Y be a continuous mapping of topological spaces, and Sh(–) the category of sheaves of abelian groups on a topological space. The direct image with compact (or proper) support

f_!: Sh(X) → Sh(Y)

sends a sheaf F on X to f_!(F) defined by

f_!(F)(U) := {s ∈ F(f⁻¹(U)) : f_|supp(s):supp(s)→U is proper},

where U is an open subset of Y. The functoriality of this construction follows from the very basic properties of the support and the definition of sheaves.

Properties

If f is proper, then f_! equals f_∗. In general, f_!(F) is only a subsheaf of f_∗(F)

References

Iversen, Birger (1986), Cohomology of sheaves, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-3-540-16389-3, MR 842190 , esp. section VII.1