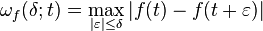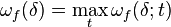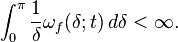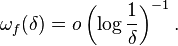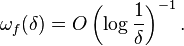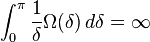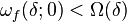Dini test

In mathematics, the Dini and Dini-Lipschitz tests are highly precise tests that can be used to prove that the Fourier series of a function converges at a given point. These tests are named after Ulisse Dini and Rudolf Lipschitz.[1]

Definition

Let f be a function on [0,2π], let t be some point and let δ be a positive number. We define the local modulus of continuity at the point t by

\left.\right.\omega_f(\delta;t)=\max_{|\varepsilon| \le \delta} |f(t)-f(t+\varepsilon)|

Notice that we consider here f to be a periodic function, e.g. if t = 0 and ε is negative then we define f(ε) = f(2π + ε).

The global modulus of continuity (or simply the modulus of continuity) is defined by

\left.\right.\omega_f(\delta) = \max_t \omega_f(\delta;t)

With these definitions we may state the main results

Theorem (Dini's test): Assume a function f satisfies at a point t that

\int_0^\pi \frac{1}{\delta}\omega_f(\delta;t)\,d\delta < \infty.

Then the Fourier series of f converges at t to f(t).

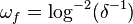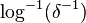For example, the theorem holds with \omega_f=\log^{-2}(\delta^{-1}) but does not hold with \log^{-1}(\delta^{-1}).

Theorem (the Dini-Lipschitz test): Assume a function f satisfies

\omega_f(\delta)=o\left(\log\frac{1}{\delta}\right)^{-1}.

Then the Fourier series of f converges uniformly to f.

In particular, any function of a Hölder class satisfies the Dini-Lipschitz test.

Precision

Both tests are best of their kind. For the Dini-Lipschitz test, it is possible to construct a function f with its modulus of continuity satisfying the test with O instead of o, i.e.

\omega_f(\delta)=O\left(\log\frac{1}{\delta}\right)^{-1}.

and the Fourier series of f diverges. For the Dini test, the statement of precision is slightly longer: it says that for any function Ω such that

\int_0^\pi \frac{1}{\delta}\Omega(\delta)\,d\delta = \infty

there exists a function f such that

\left.\right.\omega_f(\delta;0) < \Omega(\delta)

and the Fourier series of f diverges at 0.

See also

References

  1. ↑ Karl E. Gustafson (1999), Introduction to Partial Differential Equations and Hilbert Space Methods, Courier Dover Publications, p. 121, ISBN 978-0-486-61271-3