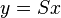Diffusionless transformation

Diffusionless transformations classifications

A diffusionless transformation is a phase change that occurs without the long-range diffusion of atoms but rather by some form of cooperative, homogeneous movement of many atoms that results in a change in crystal structure. These movements are small, usually less than the interatomic distances, and the atoms maintain their relative relationships. The ordered movement of large numbers of atoms lead some to refer to these as military transformations in contrast to civilian diffusion-based phase changes.[1]

The most commonly encountered transformation of this type is the martensitic transformation which, while being the most studied, is only one subset of non-diffusional transformations. The martensitic transformation in steel represents the most economically significant example of this category of phase transformations but an increasing number of alternatives, such as shape memory alloys, are becoming more important as well.

Classification and definitions

When a structural change occurs by the coordinated movement of atoms (or groups of atoms) relative to their neighbors then the change is termed displacive transformation. This covers a broad range of transformations and so further classifications have been developed [Cohen 1979].

The first distinction can be drawn between transformations dominated by lattice-distortive strains and those where shuffles are of greater importance.

Homogeneous lattice-distortive strains, also known as Bain strains, are strains that transform one Bravais lattice into a different one. This can be represented by a strain matrix S which transforms one vector, y, into a new vector, x:

y=Sx

This is homogeneous as straight lines are transformed to new straight lines. Examples of such transformations include a cubic lattice increasing in size on all three axes (dilation) or shearing into a monoclinic structure.

Shuffles, as the name suggests, involve the small movement of atoms within the unit cell. As a result pure shuffles do not normally result in a shape change of the unit cell - only its symmetry and structure.

Phase transformations normally result in the creation of an interface between the transformed and parent material. The energy required to generate this new interface will depend on its nature - essentially how well the two structures fit together. An additional energy term occurs if the transformation includes a shape change since, if new phase is constrained by surrounding material, this may give rise to elastic or plastic deformation and hence a strain energy term. The ratio of these interfacial and strain energy terms has a notable effect on the kinetics of the transformation and the morphology of the new phase. Thus, shuffle transformations, where distortions are small, are dominated by interfacial energies and can be usefully separated from lattice-distortive transformations where the strain energy tends to have a greater effect.

A subclassification of lattice-distortive displacements can be made by considering the dilational and shear components of the distortion. In transformations dominated by the shear component it is possible to find a line in the new phase that is undistorted from the parent phase while all lines are distorted when the dilation is predominant. Shear dominated transformations can be further classified according to the magnitude of the strain energies involved compared to the innate vibrations of the atoms in the lattice and hence whether the strain energies have a notable influence on the kinetics of the transformation and the morphology of the resulting phase. If the strain energy is a significant factor then the transformations are dubbed martensitic and if it is not the transformation is referred to as quasi-martensitic.

Martensitic transformation

The difference between austenite and martensite is, in some ways, quite small: while the unit cell of austenite is, on average, a perfect cube, the transformation to martensite distorts this cube by interstitial carbon atoms that do not have time to diffuse out during displacive transformation. The unit cell becomes slightly longer in one dimension and shorter in the other two. The mathematical description of the two structures is quite different, for reasons of symmetry (see external links), but the chemical bonding remains very similar. Unlike cementite, which has bonding reminiscent of ceramic materials, the hardness of martensite is difficult to explain in chemical terms.

The explanation hinges on the crystal's subtle change in dimension. Even a microscopic crystallite is millions of unit cells long. Since all of these units face the same direction, distortions of even a fraction of a percent become magnified into a major mismatch between neighboring materials. The mismatch is sorted out by the creation of a myriad of crystal defects, in a process reminiscent of work hardening. As in work-hardened steel, these defects prevent atoms from sliding past one another in an organized fashion, causing the material to become harder.

Shape memory alloys also have surprising mechanical properties, that were eventually explained by an analogy to martensite. Unlike the iron-carbon system, alloys in the nickel-titanium system can be chosen that make the "martensitic" phase thermodynamically stable.

Pseudomartensitic transformation

In addition to displacive transformation and diffusive transformation, a new phase transformation that involves displasive sublattice transition and atomic diffusion was discovered using a high-pressure x-ray diffraction system.[2] The new transformation mechanism has been christened a pseudomartensitic transformation.[3]

References

Notes

  1. ↑ D.A. Porter and K.E. Easterling, Phase transformations in metals and alloys, Chapman & Hall, 1992, p.172 ISBN 0-412-45030-5
  2. ↑ Jiuhua Chen, Donald J. Weidner, John B. Parise, Michael T. Vaughan, and Paul Raterron, (2001) Observation of Cation Reordering during the Olivine-Spinel Transition in Fayalite by In Situ Synchrotron X-Ray Diffraction at High Pressure and Temperature Phys. Rev. Lett, 86, pp. 4072–4075.
  3. ↑ Kristin Leutwyler New phase transition Scientific American, May 2, 2001.

Bibliography

External links