Differential graded algebra

In mathematics, in particular abstract algebra and topology, a differential graded algebra is a graded algebra with an added chain complex structure that respects the algebra structure.

Definition

A differential graded algebra (or simply DG-algebra) A is a graded algebra equipped with a map 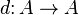which is either degree 1 (cochain complex convention) or degree 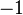(chain complex convention) that satisfies two conditions:

(i)

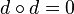
This says that d gives A the structure of a chain complex or cochain complex (accordingly as the differential reduces or raises degree).

(ii) 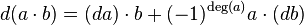, where deg is the degree.

This says that the differential d respects the graded Leibniz rule.

A DGA is an augmented DG-algebra, or differential graded augmented algebra (the terminology is due to Henri Cartan).^[1] Many sources use the term DGAlgebra for a DG-algebra.

Examples of DGAs

• The Koszul complex is a DGA.
• The Tensor algebra is a DGA with differential similar to that of the Koszul complex.
• The Singular cohomology with coefficients in a ring is a DGA; the differential is given by the Bockstein homomorphism, and the product given by the cup product.
• Differential forms on a manifold, together with the exterior derivation and the wedge-product form a DGA. See also de Rham cohomology.

Other facts about DGAs

• The homology 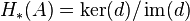of a DG-algebra 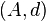is a graded algebra. The homology of a DGA is an augmented algebra.

See also

• Chain complex
• Commutative ring spectrum
• Derived scheme
• Differential graded category
• Differential graded Lie algebra
• Graded (mathematics)
• Graded algebra

References

• Manin, Yuri Ivanovich; Gelfand, Sergei I. (2003), Methods of Homological Algebra, Berlin, New York: Springer-Verlag, ISBN 978-3-540-43583-9 , see chapter V.3