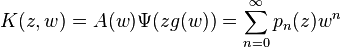Difference polynomials
In mathematics, in the area of complex analysis, the general difference polynomials are a polynomial sequence, a certain subclass of the Sheffer polynomials, which include the Newton polynomials, Selberg's polynomials, and the Stirling interpolation polynomials as special cases.
Definition
The general difference polynomial sequence is given by
where  is the binomial coefficient. For
is the binomial coefficient. For 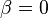 , the generated polynomials
, the generated polynomials 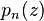 are the Newton polynomials
are the Newton polynomials
The case of 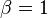 generates Selberg's polynomials, and the case of
generates Selberg's polynomials, and the case of 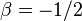 generates Stirling's interpolation polynomials.
generates Stirling's interpolation polynomials.
Moving differences
Given an analytic function 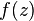 , define the moving difference of f as
, define the moving difference of f as
where 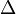 is the forward difference operator. Then, provided that f obeys certain summability conditions, then it may be represented in terms of these polynomials as
is the forward difference operator. Then, provided that f obeys certain summability conditions, then it may be represented in terms of these polynomials as
The conditions for summability (that is, convergence) for this sequence is a fairly complex topic; in general, one may say that a necessary condition is that the analytic function be of less than exponential type. Summability conditions are discussed in detail in Boas & Buck.
Generating function
The generating function for the general difference polynomials is given by
This generating function can be brought into the form of the generalized Appell representation
by setting 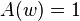 ,
, 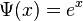 ,
, 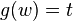 and
and 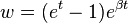 .
.
See also
References
- Ralph P. Boas, Jr. and R. Creighton Buck, Polynomial Expansions of Analytic Functions (Second Printing Corrected), (1964) Academic Press Inc., Publishers New York, Springer-Verlag, Berlin. Library of Congress Card Number 63-23263.
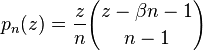
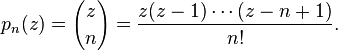
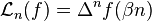
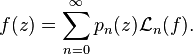
![e^{zt}=\sum_{n=0}^\infty p_n(z)
\left[\left(e^t-1\right)e^{\beta t}\right]^n.](../I/m/bca7633d1a65858d7e2edfa6adf02c00.png)