Dielectrophoresis
Dielectrophoresis (or DEP) is a phenomenon in which a force is exerted on a dielectric particle when it is subjected to a non-uniform electric field.[1][2][3][4][5][6] This force does not require the particle to be charged. All particles exhibit dielectrophoretic activity in the presence of electric fields. However, the strength of the force depends strongly on the medium and particles' electrical properties, on the particles' shape and size, as well as on the frequency of the electric field. Consequently, fields of a particular frequency can manipulate particles with great selectivity. This has allowed, for example, the separation of cells or the orientation and manipulation of nanoparticles[2][7] and nanowires. Furthermore, a study of the change in DEP force as a function of frequency can allow the electrical (or electrophysiological in the case of cells) properties of the particle to be elucidated.
Background and Properties
Although the phenomenon we now call dielectrophoresis was described in passing as far back as the early 20th century, it was only subject to serious study, named and first understood by Herbert Pohl in the 1950s.[8][9] Recently, dielectrophoresis has been revived due to its potential in the manipulation of microparticles,[2][4][5][10]nanoparticles and cells.
Dielectrophoresis occurs when a polarizable particle is suspended in a non-uniform electric field. The electric field polarizes the particle, and the poles then experience a force along the field lines, which can be either attractive or repulsive according to the orientation on the dipole. Since the field is non-uniform, the pole experiencing the greatest electric field will dominate over the other, and the particle will move. The orientation of the dipole is dependent on the relative polarizability of the particle and medium, in accordance with Maxwell–Wagner–Sillars polarization. Since the direction of the force is dependent on field gradient rather than field direction, DEP will occur in AC as well as DC electric fields; polarization (and hence the direction of the force) will depend on the relative polarizabilities of particle and medium. If the particle moves in the direction of increasing electric field, the behavior is referred to as positive DEP (sometime pDEP), if acting to move the particle away from high field regions, it is known as negative DEP (or nDEP). As the relative polarizabilities of the particle and medium are frequency-dependent, varying the energizing signal and measuring the way in which the force changes can be used to determine the electrical properties of particles; this also allows the elimination of electrophoretic motion of particles due to inherent particle charge.
Phenomena associated with dielectrophoresis are electrorotation and traveling wave dielectrophoresis (TWDEP). These require complex signal generation equipment in order to create the required rotating or traveling electric fields, and as a result of this complexity have found less favor among researchers than conventional dielectrophoresis.
Dielectrophoretic force
The simplest theoretical model is that of a homogeneous sphere surrounded by a conducting dielectric medium.[11] For a homogeneous sphere of radius  and complex permittivity
and complex permittivity  in a medium with complex permittivity
in a medium with complex permittivity  the (time-averaged) DEP force is:[4]
the (time-averaged) DEP force is:[4]
The factor in curly brackets is known as the complex Clausius-Mossotti function[2][4][5] and contains all the frequency dependence of the DEP force. Where the particle consists of nested spheres - the most common example of which is the approximation of a spherical cell composed of an inner part (the cytoplasm) surrounded by an outer layer (the cell membrane) - then this can be represented by nested expressions for the shells and the way in which they interact, allowing the properties to be elucidated where there are sufficient parameters related to the number of unknowns being sought.
For a more general field-aligned ellipsoid of radius  and length
and length 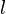 with complex dielectric constant
with complex dielectric constant 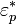 in a medium with complex dielectric constant
in a medium with complex dielectric constant 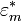 the time-dependent dielectrophoretic force is given by:[4]
the time-dependent dielectrophoretic force is given by:[4]
The complex dielectric constant is 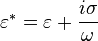 , where
, where  is the dielectric constant,
is the dielectric constant,  is the electrical conductivity,
is the electrical conductivity, 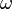 is the field frequency, and
is the field frequency, and  is the imaginary unit.[2][4][5] This expression has been useful for approximating the dielectrophoretic behavior of particles such as red blood cells (as oblate spheroids) or long thin tubes (as prolate ellipsoids) allowing the approximation of the dielectrophoretic response of carbon nanotubes or tobacco mosaic viruses in suspension.
These equations are accurate for particles when the electric field gradients are not very large (e.g., close to electrode edges) or when the particle is not moving along an axis in which the field gradient is zero (such as at the center of an axisymmetric electrode array), as the equations only take into account the dipole formed and not higher order polarization.[4] When the electric field gradients are large, or when there is a field null running through the center of the particle, higher order terms become relevant,[4] and result in higher forces.
To be precise, the time-dependent equation only applies to lossless particles, because loss creates a lag between the field and the induced dipole. When averaged, the effect cancels out and the equation holds true for lossy particles as well. An equivalent time-averaged equation can be easily obtained by replacing E with Erms, or, for sinusoidal voltages by dividing the right hand side by 2.
These models ignores the fact that cells have a complex internal structure and are heterogeneous. A multi-shell model in a low conducting medium can be used to obtain information of the membrane conductivity and the permittivity of the cytoplasm.[12]
For a cell with a shell surrounding a homogeneous core with its surrounding medium considered as a layer, as seen in Figure 2, the overall dielectric response is obtained from a combination of the properties of the shell and core.[13]
is the imaginary unit.[2][4][5] This expression has been useful for approximating the dielectrophoretic behavior of particles such as red blood cells (as oblate spheroids) or long thin tubes (as prolate ellipsoids) allowing the approximation of the dielectrophoretic response of carbon nanotubes or tobacco mosaic viruses in suspension.
These equations are accurate for particles when the electric field gradients are not very large (e.g., close to electrode edges) or when the particle is not moving along an axis in which the field gradient is zero (such as at the center of an axisymmetric electrode array), as the equations only take into account the dipole formed and not higher order polarization.[4] When the electric field gradients are large, or when there is a field null running through the center of the particle, higher order terms become relevant,[4] and result in higher forces.
To be precise, the time-dependent equation only applies to lossless particles, because loss creates a lag between the field and the induced dipole. When averaged, the effect cancels out and the equation holds true for lossy particles as well. An equivalent time-averaged equation can be easily obtained by replacing E with Erms, or, for sinusoidal voltages by dividing the right hand side by 2.
These models ignores the fact that cells have a complex internal structure and are heterogeneous. A multi-shell model in a low conducting medium can be used to obtain information of the membrane conductivity and the permittivity of the cytoplasm.[12]
For a cell with a shell surrounding a homogeneous core with its surrounding medium considered as a layer, as seen in Figure 2, the overall dielectric response is obtained from a combination of the properties of the shell and core.[13]
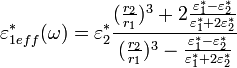
where 1 is the core (in cellular terms, the cytoplasm), 2 is the shell (in a cell, the membrane). r1 is the radius from the centre of the sphere to the inside of the shell, and r2 is the radius from the centre of the sphere to the outside of the shell.
Applications of Dielectrophoresis
Dielectrophoresis can be used to manipulate, transport, separate and sort different types of particles. Since biological cells have dielectric properties,[14][15] dielectrophoresis has many medical applications. Prototypes that separate cancer cells from healthy cells have been made.[16] Platelets have been separated from whole blood with a DEP-activated cell sorter.[17] Dielectrophoresis can be used to manipulate, transport, separate and sort different types of particles. DEP is being applied in fields such as:
- Medical diagnostics
- Drug discovery
- Cell therapeutics
- Particle filtration
The most effort in studying DEP has been directed towards satisfying the unmet needs in the biomedical sciences.
As biological cells have dielectric properties [14][15] dielectrophoresis has many medical applications. Prototypes that separate cancer cells from healthy cells have been made.[16] DEP has made it possible to characterize and manipulate biological particles like blood cells, stem cells, neurons, pancreatic β cells, DNA, chromosomes, proteins and viruses. DEP can be used to separate particles with different sign polarizabilities as they move in different directions at a given frequency of the AC field applied. DEP has been applied for the separation of:
- Live and dead cells, with the remaining live cells still viable after separation[18]
- Cancer cells from blood[19]
- Strains of bacteria and viruses[20][21]
- Red and white blood cells
DEP can also be used to detect apoptosis soon after drug induction measuring the changes in electrophysiological properties.[22]
DEP as a cell characterisation tool
DEP is mainly used for characterising cells measuring the changes in their electrical properties. To do this, many techniques are available to quantify the dielectrophoretic response, as it is not possible to directly measure the DEP force. These techniques rely on indirect measures, obtaining a proportional response of the strength and direction of the force that needs to be scaled to the model spectrum. So most models only consider the Clausius-Mossotti factor of a particle. The most used techniques are:
- Collection rate measurements: this is the simplest and most used technique. Electrodes are submerged in a suspension with a known concentration of particles and the particles that collect at the electrode are counted.[23]
- Crossover measurements: the crossover frequency between positive and negative DEP is measured to characterise particles. This technique is used for smaller particles (e.g. viruses), that are difficult to count with the previous technique.[24]
- Particle velocity measurements: this technique measures the velocity and direction of the particles in an electric field gradient.[25]
- Measurement of the levitation height: the levitation height of a particle is proportional to the negative DEP force that is applied. Thus, this technique is good for characterising single particles and is mainly used for larger particles such as cells.[26]
- Impedance sensing: particles collecting at the electrode edge have an influence on the impedance of the electrodes. This change can be monitored to quantify DEP.[27]
In order to study larger populations of cells, the properties can be obtained by analysing the dielectrophoretic spectra.[13]
Implementing Dielectrophoresis
Electrode geometries
At the start, electrodes were made mainly from wires or metal sheets. Nowadays, the electric field in DEP is created by means of electrodes which minimize the magnitude of the voltage needed. This has been possible using fabrication techniques such as photolithography, laser ablation and electron beam patterning.[28] These small electrodes allow the handling of small bioparticles. The most used electrode geometries are:
- Isometric: this geometry is effective for particle manipulation with DEP but repelled particles do not collect in well defined areas and so separation into two homogeneous groups is difficult.
- Polynomial: this new geometry produced well defined differences in regions of high and low forces and so particles could be collected by positive and negative DEP. This electrode geometry showed that the electrical field was highest at the middle of the inter-electrode gaps.[29]
- Interdigitated: this geometry is made alternating electrode fingers of opposing polarities and is mainly used for dielectrophoretic trapping and analysis.
- Crossbar: this geometry is potentially useful for networks of interconnects.[30]
DEP well electrodes
These electrodes were developed by Hoettges et al.[31] and offer a rapid and low cost way to quantify DEP.
A glass slide is attached to the bottom of the well to contain the sample. Successive conductive layers of the laminate are connected to the two phases of an AC signal so that the walls of the wells have electrodes of alternate potential, while the field gradient formed along the walls moves cells by DEP.[32] The dielectrophoretic properties of cells can be monitored by light absorption measurements: positive DEP attracts the cells to the wall of the well, thus when probed with a light beam the well the light intensity increases through the well. The opposite is true for negative DEP, in which the light beam becomes obscured by the cells. This approach offers many advantages over conventional, photolithography-based devices but reducing cost, increasing the amount of sample which can be analysed simultaneously, and the simplicity of cell motion reduced ot one dimension (where cells can only move radially towards or away from the centre of the well).
Dielectrophoresis Field-Flow Fractionation (DEP-FFF)
The utilization of the difference between dielectrophoretic forces exerted on different particles in nonuniform electric fields is known as DEP separation. The exploitation of DEP forces has been classified into two groups: DEP migration and DEP retention. DEP migration uses DEP forces that exert opposite signs of force on different particle types to attract some of the particles and repel others.[33] DEP retention uses the balance between DEP and fluid-flow forces. Particles experiencing repulsive and weak attractive DEP forces are eluted by fluid flow, whereas particles experiencing strong attractive DEP forces are trapped at electrode edges against flow drag.[34]
Dielectrophoresis Field-Flow Fractionation, introduced by Davis and Giddings,[35] is a family of chromatographic-like separation methods. In DEP-FFF, DEP forces are combined with drag flow to fractionate a sample of different types of particles.[34][36][37][38][39][40] Particles are injected into a carrier flow that passes through the separation chamber, with an external separating force (a DEP force) being applied perpendicular to the flow. By means of different factors, such as diffusion and steric, hydrodynamic, dielectric and other effects, or a combination thereof, particles (<1 μm in diameter) with different dielectric or diffusive properties attain different positions away from the chamber wall, which, in turn, exhibit different characteristic concentration profile. Particles that move further away from the wall reach higher positions in the parabolic velocity profile of the liquid flowing through the chamber and will be eluted from the chamber at a faster rate.
Optical Dielectrophoresis
The use of photoconductive materials (for example, in lab-on-chip devices) allows for localized inducement of dielectrophoretic forces through the application of light. In addition, one can project an image to induce forces in a patterned illumination area, allowing for some complex manipulations. When manipulating living cells, optical dielectrophoresis provides a non-damaging alternative to optical tweezers, as the intensity of light is about 1000 times less.[41]
References
- ↑ Pohl, H. A., 1978. Dielectrophoresis the behavior of neutral matter in nonuniform electric fields. Cambridge University Press. Cambridge.
- ↑ 2.0 2.1 2.2 2.3 2.4 Morgan, H. and Green, N. AC Electrokinetics: Colloids and Nanoparticles(Research Studies Press, 2002)
- ↑ Hughes, M.P. Nanoelectromechanics in Engineering and Biology (CRC Press, 2002)
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 T. B. Jones, Electromechanics of particles (Cambridge University Press, Cambridge, 1995).
- ↑ 5.0 5.1 5.2 5.3 Kirby, B.J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. Cambridge University Press. ISBN 978-0-521-11903-0.
- ↑ Chang, H.C. and Yao, L. (2009). Electrokinetically Driven Microfluidics and Nanofluidics.
- ↑ Hughes, M.P. ' AC Electrokinetics: Applications for Nanotechnology’ Nanotechnology 11 124-132
- ↑ H. A. Pohl, "The Motion and Precipitation of Suspensoids in Divergent Electric Fields", J. Appl. Phys. 22(7), 869–871 (1951).
- ↑ Pohl, H. A., 1958, "Some effects of nonuniform fields on dielectrics", J. Appl. Phys., 29(8), 1182 - 1188.
- ↑ Tathireddy, P.; Choi, Y-H, Skliar, M (2008). "Particle AC electrokinetics in planar interdigitated microelectrode geometry". Journal of Electrostatics 66 (11-12): 609–619. doi:10.1016/j.elstat.2008.09.002.
- ↑ Irimajiri, A., T. Hanai, and A. Inouye, Dielectric theory of multi-stratified shell-model with its application to a lymphoma cell. Journal of Theoretical Biology, 1979. 78(2): p. 251-269
- ↑ Pauly, H. and H.P. Schwan, Impedance of a suspension of ball-shaped particles with a shell: a model for the dielectric behaviour of cell suspensions and protein solutions (Uber die impedanz einer suspension von kugelformigen teilchen mit einer schale -ein modell fur das dielektrische verhalten von zellsuspensionen und von proteinlosungen). Zeitschrift Fur Naturforschung Part B-Chemie Biochemie Biophysik Biologie Und Verwandten Gebiete, 1959. 14(2): p. 125-131
- ↑ 13.0 13.1 Broche, L.M., F.H. Labeed, and M.P. Hughes, Extraction of dielectric properties of multiple populations from dielectrophoretic collection spectrum data. Physics in Medicine and Biology, 2005. 50(10): p. 2267-2274
- ↑ 14.0 14.1 Pethig R. Dielectric Properties of Biological Materials, 1979.
- ↑ 15.0 15.1 Choi, J.W., Pu, A. and Psaltis, D. (2006). "Optical detection of asymmetric bacteria utilizing electro orientation". Optics Express 14: 9780–9785. Bibcode:2006OExpr..14.9780C. doi:10.1364/OE.14.009780.
- ↑ 16.0 16.1 Micro-fluidics cut cancer test from a day to an hour - IMEC Tech Forum
- ↑ Pommer, MS et al., 2008. "Dielectrophoretic separation of platelets from diluted whole blood in microfluidic channels", Electrophoresis, 29(6), 1213-1218.
- ↑ Pohl, H.A. and I. Hawk, Separation of living and dead cells by dielectrophoresis. Science, 1966. 152(3722): p. 647-&
- ↑ Gascoyne, P.R.C., et al., Dielectrophoretic separation of cancer cells from blood. Ieee Transactions on Industry Applications, 1997. 33(3): p. 670-678
- ↑ Markx, G.H., P.A. Dyda, and R. Pethig, Dielectrophoretic separation of bacteria using a conductivity gradient. Journal of Biotechnology, 1996. 51(2): p. 175-180
- ↑ Burt, J.P.H., R. Pethig, and M.S. Talary, Microelectrode devices for manipulating and analysing bioparticles. Transactions of the Institute of Measurement and Control, 1998. 20(2): p. 82-90
- ↑ Chin, S., et al., Rapid assessment of early biophysical changes in K562 cells during apoptosis determined using dielectrophoresis. International Journal of Nanomedicine, 2006. 1(3): p. 333-337
- ↑ Labeed, F.H., Coley, H.M., Hughes, M.P. (2006), Biochim Biophys Acta 1760, 922-929
- ↑ Hughes, M.P., Morgan, H., Rixon, F.J., Burt, J.P.H., Pethig, R. (1998) , Biochim Biophys Acta 1425, 119-126
- ↑ Watarai, H., Sakomoto, T., Tsukahara, S. (1997) Langmuir 13, 2417-2420
- ↑ Kaler, K.V., Jones, T.B. (1990) Biophysical Journal 57, 173-182
- ↑ Allsop, D.W.E., Milner, K.R., Brown, A.P., Betts, W.B. (1999) Journal of Physics D: Applied Physics 32, 1066-1074
- ↑ Suehiro, J. and R. Pethig, The dielectrophoretic movement and positioning of a biological cell using a three-dimensional grid electrode system. Journal of Physics D-Applied Physics, 1998. 31(22): p. 3298-3305
- ↑ Huang, Y. and R. Pethig, Electrode design for negative dielectrophoresis. Measurement Science & Technology, 1991. 2(12): p. 1142-1146
- ↑ A. D. Wissner-Gross, "Dielectrophoretic architectures", Bio-Inspired and Nanoscale Integrated Computing 155-173 (ed. M. Eshaghian-Wilner, Wiley, 2009).
- ↑ Hoettges, K.F., et al., Dielectrophoresis-activated multiwell plate for label-free high-throughput drug assessment. Analytical Chemistry, 2008. 80(6): p. 2063-2068
- ↑ Fatoyinbo, H.O., et al., A high-throughput 3-D composite dielectrophoretic separator. IEEE Transactions on Biomedical Engineering, 2005. 52(7): p. 1347-1349
- ↑ A. D. Wissner-Gross, "Dielectrophoretic reconfiguration of nanowire interconnects", Nanotechnology 17, 4986-4990 (2006).
- ↑ 34.0 34.1 Gascoyne, P.R.C., Y. Huang, R. Pethig, J. Vykoukal and F.F. Becker, 1992. "Dielectrophoretic separation of mammalian cells studied by computerized image analysis". Meas. Sci.Technol. 3, 439-445.
- ↑ Davis, J.M. and J.C. Giddings, 1986. "Feasibility study of dielectrical field-flow fractionation". Sepa. Sci. and Tech. 21, 969-989.
- ↑ Giddings, J.C., 1993. "Field-Flow Fractionation: Analysis of macromolecular, colloidal, and particulate materials". Science. 260, 1456-1465.
- ↑ G.H. Markx, J. Rousselet and R. Pethig, 1997. "DEP-FFF: Field-flow fractionation using non-uniform electric fields." Journal of Liquid Chromatography & Related Technologies 20, 2857-2872
- ↑ Huang, Y., X.B. Wang, F.F. Becker and P.R.C. Gascoyne, 1997. "Introducing dielectrophoresis as a new force field for field-flow fractionation". Biophys. J. 73, 1118-1129
- ↑ Wang, X.B., J. Vykoukal, F.F. Becker and P.R.C. Gascoyne, 1998. "Separation of polystyrene microbeads using dielectrophoretic/gravitational field-flow-fractionation". Biophysical Journal. 74, 2689-2701.
- ↑ Rousselet, G.H. Markx & R. Pethig, 1998 "Separation of erythrocytes and latex beads by dielectrophoretic levitation and hyperlayer field-flow fractionation." Colloids and Surfaces A. 140, 209-216
- ↑ Dongqing Li, ed. "Encyclopedia of Microfluidics and Nanofluidics". Springer, New York, 2008.
External links
- The American Electrophoresis Society: Dielectrophoresis
- Dielectrophoresis: a spherical shell model
- On the Relationship of Dielectrophoresis and Electrowetting
- Biological cell separation using dielectrophoresis in a microfluidic device
- Sandia’s dielectrophoresis device may revolutionize sample preparation
- Institute of Bioelectronic and Molecular Microsystems: Dielectrophoresis