Deviation risk measure

In financial mathematics, a deviation risk measure is a function to quantify financial risk (and not necessarily downside risk) in a different method than a general risk measure. Deviation risk measures generalize the concept of standard deviation.

Mathematical definition

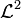A function $D: \mathcal{L}^2 \to [0,+\infty]$ , where $\mathcal{L}^2$ is the L2 space of random portfolio returns, is a deviation risk measure if

Shift-invariant: 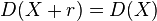$D(X + r) = D(X)$ for any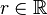 $r \in \mathbb{R}$
Normalization: $D(0) = 0$
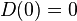
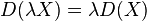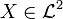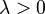
Positively homogeneous: $D(\lambda X) = \lambda D(X)$ for any $X \in \mathcal{L}^2$ and $\lambda > 0$
Sublinearity: 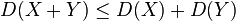$D(X + Y) \leq D(X) + D(Y)$ for any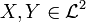 $X, Y \in \mathcal{L}^2$
Positivity: 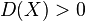$D(X) > 0$ for all nonconstant X, and 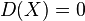$D(X) = 0$ for any constant X.^[1]^[2]

Relation to risk measure

There is a one-to-one relationship between a deviation risk measure D and an expectation-bounded risk measure R where for any 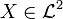$X \in \mathcal{L}^2$

$D(X) = R(X - \mathbb{E}[X])$
$R(X) = D(X) - \mathbb{E}[X]$ .

R is expectation bounded if $R(X) > \mathbb{E}[-X]$ for any nonconstant X and $R(X) = \mathbb{E}[-X]$ for any constant X.

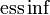If $D(X) < \mathbb{E}[X] - \operatorname{ess\inf} X$ for every X (where $\operatorname{ess\inf}$ is the essential infimum), then there is a relationship between D and a coherent risk measure.^[1]

Examples

The standard deviation is clearly a deviation risk measure.

References

↑ 1.0 1.1 Rockafellar, Tyrrell; Uryasev, Stanislav; Zabarankin, Michael (2002). "Deviation Measures in Risk Analysis and Optimization". Retrieved January 15, 2012.
↑ Cheng, Siwei; Liu, Yanhui; Wang, Shouyang (2004). "Progress in Risk Measurement". Advanced Modelling and Optimization 6 (1).