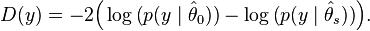Deviance (statistics)
In statistics, deviance is a quality of fit statistic for a model that is often used for statistical hypothesis testing. It is a generalization of the idea of using the sum of squares of residuals in ordinary least squares to cases where model-fitting is achieved by maximum likelihood.
Definition
The deviance for a model M0, based on a dataset y, is defined as:[1][2]
Here 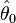 denotes the fitted values of the parameters in the model M0, while
denotes the fitted values of the parameters in the model M0, while 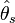 denotes the fitted parameters for the "full model" (or "saturated model"): both sets of fitted values are implicitly functions of the observations y. Here the full model is a model with a parameter for every observation so that the data are fitted exactly. This expression is simply −2 times the log-likelihood ratio of the reduced model compared to the full model. The deviance is used to compare two models – in particular in the case of generalized linear models where it has a similar role to residual variance from ANOVA in linear models (RSS).
denotes the fitted parameters for the "full model" (or "saturated model"): both sets of fitted values are implicitly functions of the observations y. Here the full model is a model with a parameter for every observation so that the data are fitted exactly. This expression is simply −2 times the log-likelihood ratio of the reduced model compared to the full model. The deviance is used to compare two models – in particular in the case of generalized linear models where it has a similar role to residual variance from ANOVA in linear models (RSS).
Suppose in the framework of the GLM, we have two nested models, M1 and M2. In particular, suppose that M1 contains the parameters in M2, and k additional parameters. Then, under the null hypothesis that M2 is the true model, the difference between the deviances for the two models follows an approximate chi-squared distribution with k-degrees of freedom.[2]
Some usage of the term "deviance" can be confusing. According to Collett:[3]
- "the quantity
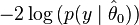 is sometimes referred to as a deviance. This is [...] inappropriate, since unlike the deviance used in the context of generalized linear modelling,
is sometimes referred to as a deviance. This is [...] inappropriate, since unlike the deviance used in the context of generalized linear modelling, 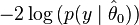 does not measure deviation from a model that is a perfect fit to the data." However, since the principal use is in the form of the difference of the deviances of two models, this confusion in definition is unimportant.
does not measure deviation from a model that is a perfect fit to the data." However, since the principal use is in the form of the difference of the deviances of two models, this confusion in definition is unimportant.
See also
- Pearson's chi-squared test, an alternative quality of fit statistic for generalized linear models for count data.
- Hosmer–Lemeshow test, a quality of fit statistic that can be used for binary data.
- Akaike information criterion
- Deviance information criterion
- Peirce's criterion
- Discrepancy function
Notes
- ↑ Nelder, J.A.; Wedderburn, R.W.M. (1972). "Generalized Linear Models". Journal of the Royal Statistical Society. Series A (General) 135 (3): 370–384. doi:10.2307/2344614. JSTOR 2344614.
- ↑ 2.0 2.1 McCullagh and Nelder (1989)
- ↑ Collett (2003)Template:Page 76
References
- McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Second Edition. Chapman & Hall/CRC. ISBN 0-412-31760-5.
- Collett, David (2003). Modelling Survival Data in Medical Research, Second Edition. Chapman & Hall/CRC. ISBN 1-58488-325-1.
External links
- Generalized Linear Models - Edward F. Connor
- Lectures notes on Deviance
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||