Descent direction
In optimization, a descent direction is a vector 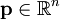 that, in the sense below, moves us closer towards a local minimum
that, in the sense below, moves us closer towards a local minimum 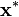 of our objective function
of our objective function 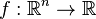 .
.
Suppose we are computing 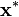 by an iterative method, such as line search. We define a descent direction
by an iterative method, such as line search. We define a descent direction 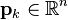 at the
at the 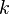 th iterate to be any
th iterate to be any 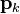 such that
such that 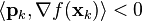 , where
, where 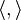 denotes the inner product. The motivation for such an approach is that small steps along
denotes the inner product. The motivation for such an approach is that small steps along 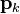 guarantee that
guarantee that 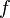 is reduced, by Taylor's theorem.
is reduced, by Taylor's theorem.
Using this definition, the negative of a non-zero gradient is always a
descent direction, as  .
.
Numerous methods exist to compute descent directions, all with differing merits. For example, one could use gradient descent or the conjugate gradient method.
More generally, if  is a positive definite matrix, then
is a positive definite matrix, then
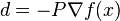 is a descent direction
[1]
at
is a descent direction
[1]
at 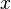 .
This generality is used in preconditioned gradient descent methods.
.
This generality is used in preconditioned gradient descent methods.
- ↑ J. M. Ortega and W. C. Rheinbold (1970). Iterative Solution of Nonlinear Equations in Several Variables. p. 243. doi:10.1137/1.9780898719468.