Derived scheme

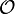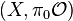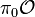In algebraic geometry, a derived scheme is a pair $(X, \mathcal{O})$ consisting of a topological space X and a sheaf $\mathcal{O}$ of commutative ring spectra ^[1] on X such that (1) the pair $(X, \pi_0 \mathcal{O})$ is a scheme and (2) $\pi_k \mathcal{O}$ is a quasi-coherent $\pi_0 \mathcal{O}$ -module. The notion gives a homotopy-theoretic generalization of a scheme.

Connection with differential graded rings

Just as affine algebraic geometry is equivalent (in categorical sense) to the theory of commutative rings (commonly called commutative algebra), affine derived algebraic geometry is (roughly in homotopical sense) equivalent to the theory of commutative differential graded rings.

Generalizations

A derived stack is a stacky generalization of a derived scheme.

Notes

↑ also often called 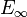$E_\infty$ -ring spectra

References

P. Goerss, Topological Modular Forms [after Hopkins, Miller, and Lurie]
B. Toën, Introduction to derived algebraic geometry