Deltoidal hexecontahedron
| Deltoidal hexecontahedron | |
|---|---|
 click for spinning version | |
| Type | Catalan |
| Conway notation | oD or deD |
| Coxeter diagram | |
| Face polygon |  kite |
| Faces | 60 |
| Edges | 120 |
| Vertices | 62 = 12 + 20 + 30 |
| Face configuration | V3.4.5.4 |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 154° 7' 17" |
| Properties | convex, face-transitive |
 rhombicosidodecahedron (dual polyhedron) |
 Net |
In geometry, a deltoidal hexecontahedron (also sometimes called a trapezoidal hexecontahedron, a strombic hexecontahedron, or a tetragonal hexacontahedron[1]) is a catalan solid which looks a bit like either an overinflated dodecahedron or icosahedron. It is sometimes also called the trapezoidal hexecontahedron or strombic hexecontahedron. Its dual polyhedron is the rhombicosidodecahedron.
The 60 faces are deltoids or kites (not trapezoidal). The short and long edges of each kite are in the ratio 1.00:1.54.
It is the only Archimedean dual which does not have a Hamiltonian path among its vertices.
Orthogonal projections
The deltoidal hexecontahedron has 3 symmetry positions located on the 3 types of vertices:
| Projective symmetry |
[2] | [6] | [10] |
|---|---|---|---|
| Image | 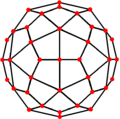 |
 |
 |
| Dual image |
 |
 |
 |
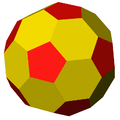
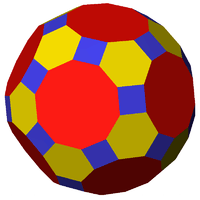
Related polyhedra and tilings

| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
| {5,3} | t{5,3} | r{5,3} | 2t{5,3}=t{3,5} | 2r{5,3}={3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
This tiling is topologically related as a part of sequence of deltoidal polyhedra with face figure (V3.4.n.4), and continues as tilings of the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | [3i,3] | ||
| Figure |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| Schläfli | rr{2,3} | rr{3,3} | rr{4,3} | rr{5,3} | rr{6,3} | rr{7,3} | rr{8,3} | rr{∞,3} | rr{12i,3} | rr{9i,3} | rr{6i,3} | rr{3i,3} | |
| Coxeter | |||||||||||||
| Dual uniform figures | |||||||||||||
| Dual Config. |
 V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
 V3.4.∞.4 |
V3.4.12i.4 | V3.4.9i.4 | V3.4.6i.4 | V3.4.3i.4 | |
| Coxeter | |||||||||||||
See also
References
- ↑ Conway, Symmetries of things, p.284-286
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 286, tetragonal hexecontahedron)
External links
- Eric W. Weisstein, DeltoidalHexecontahedron and Hamiltonian path (Catalan solid) at MathWorld
- Deltoidal Hexecontahedron (Trapezoidal Hexecontrahedron)—Interactive Polyhedron Model
- Example in real life—A ball almost 4 meters in diameter, from ripstop nylon, and inflated by the wind. It bounces around on the ground so that kids can play with it at kite festivals.
| ||||||||||||||||||||||||||||||||||||