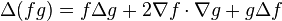Del in cylindrical and spherical coordinates
| | Help resolve this verification problem at Wikiversity. |
This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.
Notes
- This article uses the standard notation ISO 80000-2, which supersedes ISO 31-11, for spherical coordinates (other sources may reverse the definitions of θ and ϕ):
- The polar angle is denoted by θ: it is the angle between the z-axis and the radial vector connecting the origin to the point in question.
- The azimuthal angle is denoted by ϕ: it is the angle between the x-axis and the projection of the radial vector onto the xy-plane.
- The function atan2(y, x) can be used instead of the mathematical function arctan(y/x) owing to its domain and image. The classical arctan function has an image of (−π/2, +π/2), whereas atan2 is defined to have an image of (−π, π].
Formulae
| Operation | Cartesian coordinates (x, y, z) | Cylindrical coordinates (ρ, ϕ, z) | Spherical coordinates (r, θ, ϕ) | Parabolic cylindrical coordinates (σ, τ, z) |
|---|---|---|---|---|
| Definition of coordinates |
 |
 |
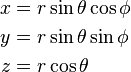 |
 |
 |
 |
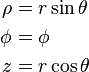 |
 | |
| Definition of unit vectors |
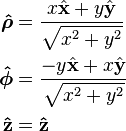 |
 |
 |
 |
 |
 |
 |
 | |
A vector field 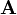 |
 |
 |
 |
 |
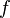 scalar field Gradient scalar field Gradient 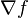 |
 |
 |
 |
 |
Divergence  |
 |
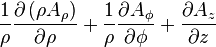 |
 |
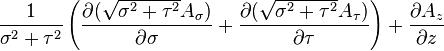 |
Curl  |
 |
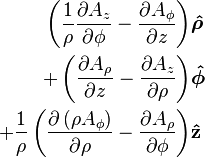 |
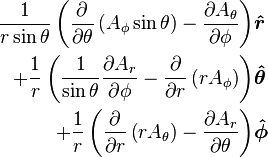 |
 |
Laplace operator  |
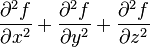 |
 |
 |
 |
Vector Laplacian  |
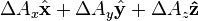 |
|
| |
| Material derivative[1]
|
 |
|
| |
| Differential displacement |  |
 |
 |
 |
Differential normal area  |
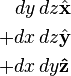 |
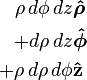 |
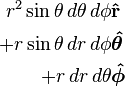 |
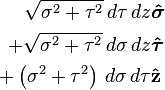 |
Differential volume 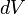 |
 |
 |
 |
 |
Non-trivial calculation rules:
| ||||
See also
- Del
- Orthogonal coordinates
- Curvilinear coordinates
- Vector fields in cylindrical and spherical coordinates
References
- ↑ Weisstein, Eric W. "Convective Operator". Mathworld. Retrieved 23 March 2011.
External links
- Maxima Computer Algebra system scripts to generate some of these operators in cylindrical and spherical coordinates.
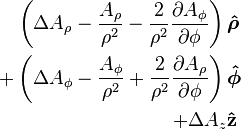
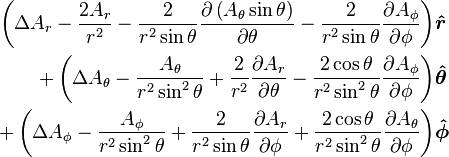
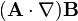

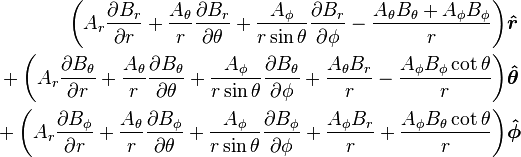

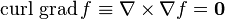

 (
(