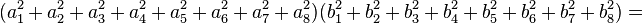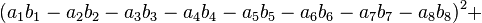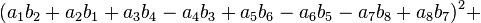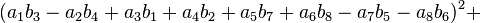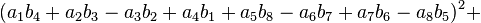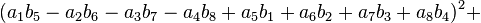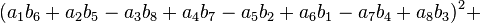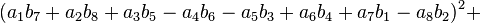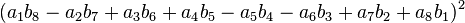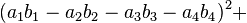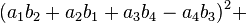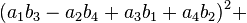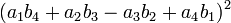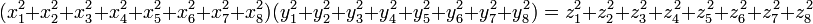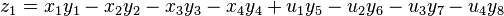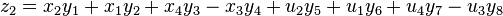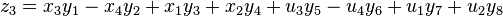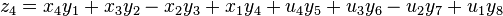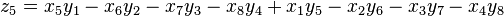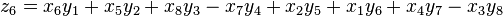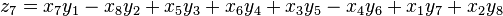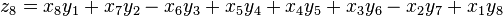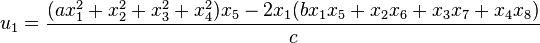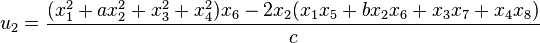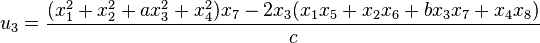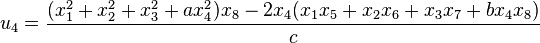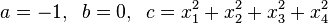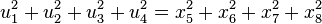Degen's eight-square identity
In mathematics, Degen's eight-square identity establishes that the product of two numbers, each of which being a sum of eight squares, is itself the sum of eight squares. Namely:
First discovered by Ferdinand Degen (Danish) around 1818, the identity was independently rediscovered by John Thomas Graves (1843) and Arthur Cayley (1845). The latter two derived it while working on an extension of quaternions called octonions. In algebraic terms the identity means that the norm of product of two octonions equals the product of their norms: 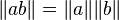 . Similar statements are true for quaternions (Euler's four-square identity), complex numbers (the Brahmagupta–Fibonacci two-square identity) and real numbers. In 1898 Adolf Hurwitz proved that there is no similar bilinear identity for 16 squares (sedenions) or any other number of squares except for 1,2,4, and 8. However, in the 1960s, H. Zassenhaus, W. Eichhorn, and A. Pfister (independently) showed there can be a non-bilinear identity for 16 squares.
. Similar statements are true for quaternions (Euler's four-square identity), complex numbers (the Brahmagupta–Fibonacci two-square identity) and real numbers. In 1898 Adolf Hurwitz proved that there is no similar bilinear identity for 16 squares (sedenions) or any other number of squares except for 1,2,4, and 8. However, in the 1960s, H. Zassenhaus, W. Eichhorn, and A. Pfister (independently) showed there can be a non-bilinear identity for 16 squares.
Note that each quadrant reduces to a version of Euler's four-square identity:
and similarly for the other three quadrants. By Pfister's theorem, a different sort of eight-square identity can be given where the 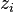 , introduced below, are non-bilinear and merely rational functions of the
, introduced below, are non-bilinear and merely rational functions of the 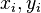 . Thus,
. Thus,
where,
and,
with,
Incidentally, the 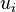 obey the identity,
obey the identity,