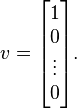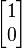Defective matrix

In linear algebra, a defective matrix is a square matrix that does not have a complete basis of eigenvectors, and is therefore not diagonalizable. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors.[1] A complete basis is formed by augmenting the eigenvectors with generalized eigenvectors, which are necessary for solving defective systems of ordinary differential equations and other problems.

A defective matrix always has fewer than n distinct eigenvalues, since distinct eigenvalues always have linearly independent eigenvectors. In particular, a defective matrix has one or more eigenvalues λ with algebraic multiplicity 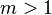m > 1 (that is, they are multiple roots of the characteristic polynomial), but fewer than m linearly independent eigenvectors associated with λ.[1] However, every eigenvalue with multiplicity m always has m linearly independent generalized eigenvectors.

A Hermitian matrix (or the special case of a real symmetric matrix) or a unitary matrix is never defective; more generally, a normal matrix (which includes Hermitian and unitary as special cases) is never defective.

Jordan block

Any Jordan block of size 2×2 or larger is defective. For example, the n × n Jordan block,

J = \begin{bmatrix} \lambda & 1 & \; & \; \\ \; & \lambda & \ddots & \; \\ \; & \; & \ddots & 1 \\ \; & \; & \; & \lambda \end{bmatrix},

has an eigenvalue, λ, with multiplicity n, but only one distinct eigenvector,

v = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}.

Example

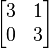
A simple example of a defective matrix is:

\begin{bmatrix} 3& 1 \\ 0 & 3 \end{bmatrix}

which has a double eigenvalue of 3 but only one distinct eigenvector

\begin{bmatrix} 1 \\ 0 \end{bmatrix}

(and constant multiples thereof).

See also

Notes

  1. ↑ 1.0 1.1 Golub & Van Loan (1996, p. 316)

References