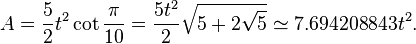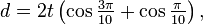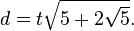Decagon

Regular decagon

A regular decagon
Type Regular polygon
Edges and vertices 10
Schläfli symbol {10}
t{5}
Coxeter diagram
Symmetry group Dihedral (D10), order 2×10
Internal angle (degrees) 144°
Dual polygon self
Properties convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a decagon is any polygon with ten sides and ten angles.[1]

A regular decagon has all sides of equal length and each internal angle equal to 144°.[1] Its Schläfli symbol is {10} [2] and can also be constructed as a quasiregular truncated pentagon, t{5}, which alternates two types of edges.

Regular decagon

The area of a regular decagon is: (with t = edge length)[3]

A = \frac{5}{2}t^2 \cot \frac{\pi}{10} = \frac{5t^2}{2} \sqrt{5+2\sqrt{5}} \simeq 7.694208843 t^2.

An alternative formula is 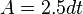A=2.5dt where d is the distance between parallel sides, or the height when the decagon stands on one side as base, or the diameter of the decagon's inscribed circle. By simple trigonometry,

d=2t\left(\cos\tfrac{3\pi}{10}+\cos\tfrac{\pi}{10}\right),

and it can be written algebraically as

d=t\sqrt{5+2\sqrt{5}}.

Sides

The side of a regular decagon inscribed in a unit circle is 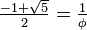\tfrac{-1+\sqrt{5}}{2}=\tfrac{1}{\phi}, where ϕ is the golden ratio, 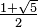\tfrac{1+\sqrt{5}}{2}.[4]

Construction

A regular decagon is constructible using compass and straightedge. See File:Regular Decagon Inscribed in a Circle.gif. [4]

An alternative (but similar) method is as follows:

  1. Construct a pentagon in a circle by one of the methods shown in constructing a pentagon.
  2. Extend a line from each vertex of the pentagon through the center of the circle to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon.
  3. The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon.

Petrie polygons

The regular decagon is the Petrie polygon for many higher-dimensional polytopes, shown in these skew orthogonal projections in various Coxeter planes:[5] The number of sides in the Petrie polygon is equal to the Coxeter number, h, for each symmetry family.

H3  

Dodecahedron
Icosahedron
Icosidodecahedron
Rhombic triacontahedron
A9 D6 B5

9-simplex
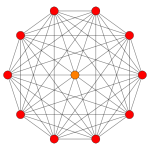411
131
5-orthoplex
5-cube

See also

References

  1. ↑ 1.0 1.1 Sidebotham, Thomas H. (2003), The A to Z of Mathematics: A Basic Guide, John Wiley & Sons, p. 146, ISBN 9780471461630.
  2. ↑ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595.
  3. ↑ The elements of plane and spherical trigonometry, Society for Promoting Christian Knowledge, 1850, p. 59. Note that this source uses a as the edge length and gives the argument of the cotangent as an angle in degrees rather than in radians.
  4. ↑ 4.0 4.1 Ludlow, Henry H. (1904), Geometric Construction of the Regular Decagon and Pentagon Inscribed in a Circle, The Open Court Publishing Co..
  5. ↑ Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.

External links