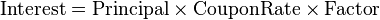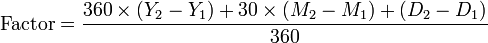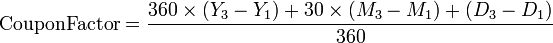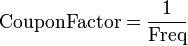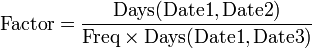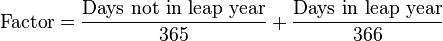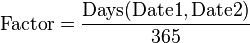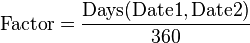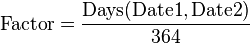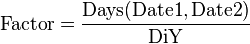Day count convention

In finance, a day count convention determines how interest accrues over time for a variety of investments, including bonds, notes, loans, mortgages, medium-term notes, swaps, and forward rate agreements (FRAs). This determines the number of days between two coupon payments; thus, calculating the amount transferred on payment dates and also the accrued interest for dates between payments.^[1] The day count is also used to quantify periods of time when discounting a cash-flow to its present value. When a security such as a bond is sold between interest payment dates, the seller is eligible to some fraction of the coupon amount.

The day count convention is used in many other formulas in financial mathematics as well.

Development

The need for day count conventions is a direct consequence of interest-earning investments. Different conventions were developed to address often conflicting requirements, including ease of calculation, constancy of time period (day, month, or year) and the needs of the Accounting department. This development occurred long before the advent of computers.

There is no central authority defining day count conventions, so there is no standard terminology, however the International Swaps and Derivatives Association (ISDA) and the International Capital Market Association (ICMA) have done work gathering and documenting conventions. Certain terms, such as "30/360", "Actual/Actual", and "money market basis" must be understood in the context of the particular market.

The conventions have evolved, and this is particularly true since the mid-1990s. Part of it has simply been providing for additional cases^[2] or clarification.^[3]

There has also been a move towards convergence in the marketplace, which has resulted in the number of conventions in use being reduced. Much of this has been driven by the introduction of the euro.^[4][5]

Definitions

Interest

Amount of interest accrued on an investment.

CouponFactor

The Factor to be used when determining the amount of interest paid by the issuer on coupon payment dates. The periods may be regular or irregular.

CouponRate

The interest rate on the security or loan-type agreement, e.g., 5.25%. In the formulas this would be expressed as 0.0525.

Date1 (Y1.M1.D1)

Starting date for the accrual. It is usually the coupon payment date preceding Date2.

Date2 (Y2.M2.D2)

Date through which interest is being accrued. You could word this as the "to" date, with Date1 as the "from" date. For a bond trade, it is the settlement date of the trade.

Date3 (Y3.M3.D3)

The coupon payment date following Date2. This would be the maturity date if there are no more interim payments to be made.

Days(StartDate, EndDate)

Function returning the number of days between StartDate and EndDate on a Julian basis (i.e., all days are counted). For instance, Days(15 October 2007, 15 November 2007) returns 31.

EOM

Indicates that the investment always pays interest on the last day of the month. If the investment is not EOM, it will always pay on the same day of the month (e.g., the 10th).

Factor

Figure representing the amount of the CouponRate to apply in calculating Interest. It is often expressed as "days in the accrual period / days in the year". If Date2 is a coupon payment date, Factor is zero.

Freq

The coupon payment frequency. 1 = annual, 2 = semi-annual, 4 = quarterly, 12 = monthly, etc.

Principal

Par value of the investment.

For all conventions, the Interest is calculated as:

30/360 methods

All conventions of this class calculate the Factor as:

They calculate the CouponFactor as:

This is the same as the Factor calculation, with Date2 replaced by Date3. In the case that it is a regular coupon period, this is equivalent to:

The conventions are distinguished by the manner in which they adjust Date1 and/or Date2 for the end of the month. Each convention has a set of rules directing the adjustments.

Treating a month as 30 days and a year as 360 days was devised for its ease of calculation by hand compared with manually calculating the actual days between two dates. Also, because 360 is highly factorable, payment frequencies of semi-annual and quarterly and monthly will be 180, 90, and 30 days of a 360 day year, meaning the payment amount will not change between payment periods.

30/360 Bond Basis

This convention is exactly as 30U/360 below, except for the first two rules. Note that the order of calculations is important:

• D1 = MIN (D1, 30).
• If D1 = 30 Then D2 = MIN (D2,30)

Other names:

• 30A/360.

Sources:

• ISDA 2006 Section 4.16(f), though the first two rules are not included.^[6]

30/360 US

Date adjustment rules (more than one may take effect; apply them in order, and if a date is changed in one rule the changed value is used in the following rules):

• If the investment is EOM and (Date1 is the last day of February) and (Date2 is the last day of February), then change D2 to 30.
• If the investment is EOM and (Date1 is the last day of February), then change D1 to 30.
• If D2 is 31 and D1 is 30 or 31, then change D2 to 30.
• If D1 is 31, then change D1 to 30.

This convention is used for US corporate bonds and many US agency issues. It is most commonly referred to as "30/360", but the term "30/360" may also refer to any of the other conventions of this class, depending on the context.

Other names:

• 30U/360 - 30U/360 is not strictly the same as 30/360, it is used for the Euribor (Euro denominated Libor) curve and Euro denominated swaps, with the distinction that under 30/360, each day in a 31 day month accrues 30/31 of interest, whereas in 30U/360 payment occurs on the 30th and the 31st is considered to be part of the next month. - Bloomberg
• Bond basis
• 30/360

Sources:

• ISDA 2006 Section 4.16(f), though the first two rules are not included.^[6]
• (Mayle 1993)

30E/360

Date adjustment rules:

• If D1 is 31, then change D1 to 30.
• If D2 is 31, then change D2 to 30.

Other names:

• 30/360 ICMA
• 30S/360
• Eurobond basis (ISDA 2006)
• Special German

Sources:

• ICMA Rule 251.1(ii), 251.2.^[7]
• ISDA 2006 Section 4.16(g).^[6]

30E/360 ISDA

Date adjustment rules:

• If D1 is the last day of the month, then change D1 to 30.
• If D2 is the last day of the month (unless Date2 is the maturity date and M2 is February), then change D2 to 30.

Other names:

• 30E/360 ISDA
• Eurobond basis (ISDA 2000)
• German

Sources:

• ISDA 2006 Section 4.16(h).^[6]

Actual methods

The conventions of this class calculate the number of days between two dates (e.g., between Date1 and Date2) as the Julian difference. This is the function Days(StartDate, EndDate).

The conventions are distinguished primarily by the amount of the CouponRate they assign to each day of the accrual period.

Actual/Actual ICMA

Formulas:

For regular coupon periods:

For irregular coupon periods, the period has to be divided into one or more quasi-coupon periods (also called notional periods) that match the normal frequency of payment dates. The interest in each such period (or partial period) is then computed, and then the amounts are summed over the number of quasi-coupon periods. For details, see (Mayle 1993) or the ISDA paper.^[4]

This method ensures that all coupon payments are always for the same amount.

It also ensures that all days in a coupon period are valued equally. However, the coupon periods themselves may be of different lengths; in the case of semi-annual payment on a 365 day year, one period can be 182 days and the other 183 days. In that case, all the days in one period will be valued 1/182nd of the payment amount and all the days in the other period will be valued 1/183rd of the payment amount.

This is the convention used for US Treasury bonds and notes, among other securities.

Other names:

• Actual/Actual
• Act/Act ICMA
• ISMA-99
• Act/Act ISMA

Sources:

• ICMA Rule 251.1(iii).^[7]
• ISDA 2006 Section 4.16(c).^[6]
• (Mayle 1993)
• Actual/Actual comparison, EMU and Market Conventions: Recent Developments.^[4]

Actual/Actual ISDA

Formulas:

This convention accounts for days in the period based on the portion in a leap year and the portion in a non-leap year.

The days in the numerators are calculated on a Julian day difference basis. In this convention the first day of the period is included and the last day is excluded.

The CouponFactor uses the same formula, replacing Date2 by Date3. In general, coupon payments will vary from period to period, due to the differing number of days in the periods. The formula applies to both regular and irregular coupon periods.

Other names are:

• Actual/Actual
• Act/Act
• Actual/365
• Act/365

Sources:

• ISDA 2006 Section 4.16(b).^[6]

Actual/365 Fixed

Formulas:

Each month is treated normally and the year is assumed to be 365 days. For example, in a period from February 1, 2005 to April 1, 2005, the Factor is considered to be 59 days divided by 365.

The CouponFactor uses the same formula, replacing Date2 by Date3. In general, coupon payments will vary from period to period, due to the differing number of days in the periods. The formula applies to both regular and irregular coupon periods.

Other names:

• Act/365 Fixed
• A/365 Fixed
• A/365F
• English

Sources:

• ISDA 2006 Section 4.16(d).^[6]
• (Mayle 1993)

Actual/360

Formulas:

This convention is used in money markets for short-term lending of currencies, including the US dollar and Euro, and is applied in ESCB monetary policy operations. It is the convention used with Repurchase agreements. Each month is treated normally and the year is assumed to be 360 days. For example, in a period from February 1, 2005 to April 1, 2005, the Factor is 59 days divided by 360 days.

The CouponFactor uses the same formula, replacing Date2 by Date3. In general, coupon payments will vary from period to period, due to the differing number of days in the periods. The formula applies to both regular and irregular coupon periods.

Other names:

• Act/360
• A/360
• French

Sources:

• ICMA Rule 251.1(i) (not sterling).^[7]
• ISDA 2006 Section 4.16(e).^[6]
• (Mayle 1993)

Actual/364

Formulas:

Each month is treated normally and the year is assumed to be 364 days. For example, in a period from February 1, 2005 to April 1, 2005, the Factor is considered to be 59 days divided by 364.

The CouponFactor uses the same formula, replacing Date2 by Date3. In general, coupon payments will vary from period to period, due to the differing number of days in the periods. The formula applies to both regular and irregular coupon periods.

Actual/365L

Formulas:

This convention requires a set of rules in order to determine the days in the year (DiY).

• If Freq = 1 (annual coupons):
  • If February 29 is in the range from Date1 (exclusive) to Date3 (inclusive), then DiY = 366, else DiY = 365.
• If Freq <> 1:
  • If Date3 is in a leap year, then DiY = 366, else DiY = 365.

The CouponFactor uses the same formula, replacing Date2 by Date3. In general, coupon payments will vary from period to period, due to the differing number of days in the periods. The formula applies to both regular and irregular coupon periods.

Other names:

• ISMA-Year

Sources:

• ICMA Rule 251.1(i) (Euro-sterling floating-rate notes).^[7]

Actual/Actual AFB

Formulas:

This convention requires a set of rules in order to determine the days in the year (DiY).

The basic rule is that if February 29 is in the range from Date1 (inclusive) to Date2 (exclusive), then DiY = 366, else DiY = 365.

If the period from Date1 to Date2 is more than one year, the calculation is split into two parts:

• the number of complete years, counted back from the last day of the period
• the remaining initial stub, calculated using the basic rule.

As an example, a period from 1994-02-10 to 1997-06-30 is split as follows:

• 1994-06-30 to 1997-06-30 = 3 (whole years calculated backwards from the end)
• 1994-02-10 to 1994-06-30 = 140/365

Resulting in a total value of 3 + 140/365.

This convention was originally written in French and during translation the term "Période d'Application" was converted to "Calculation Period". As ISDA assigns a very specific meaning to "Calculation Period" (Date1 to Date3) confusion can ensue. Reading the original French, the period referred to is Date1 to Date2, not Date1 to Date3.^[8]

The original French version of the convention contained no specific rules for counting back the years. A later ISDA paper ^[4] added an additional rule: "When counting backwards for this purpose, if the last day of the relevant period is 28 February, the full year should be counted back to the previous 28 February unless 29 February exists, in which case, 29 February should be used". No source can be found explaining the appearance or rationale of the extra rule. The table below compares the later ISDA count back rule to a simple count back rule (which would have been implied by the original French) for one of the few cases where they differ. The simple rule illustrated here is based on subtraction of n years from Date2, where subtracting whole years from a date goes back to the same day-of-month, except if starting on 29 February and going back to a non-leap year then 28 February results.

Date range	ISDA count back rule	Simple count back rule
From 2004-02-28 to 2008-02-27	3 + 365 / 366	3 + 365 / 366
From 2004-02-28 to 2008-02-28	4 + 1 / 366	4
From 2004-02-28 to 2008-02-29	4 + 1 / 366	4 + 1 / 366

Sources:

• "Definitions Communes plusieurs Additifs Techniques", by the Association Francaise des Banques in September 1994.^[8]
• FBF Master Agreement for Financial Transactions, Supplement to the Derivatives Annex, Edition 2004, section 7i.^[9]
• Actual/Actual comparison, EMU and Market Conventions: Recent Developments.^[4]

1/1

This is used for inflation instruments and divides the overall 4 year period distributing the additional day across all 4 years i.e. giving 365.25 days to each year.

Sources:

• ISDA 2006 Section 4.16(a).^[6]
• FBF Master Agreement for Financial Transactions, Supplement to the Derivatives Annex, Edition 2004, section 7a.^[9]

Discussion

Comparison of 30/360 and Actual/360

The 30/360 methods assume every month has 30 days and each year has 360 days. The 30/360 calculation is listed on standard loan constant charts and is now typically used by a calculator or computer in determining mortgage payments. This method of treating a month as 30 days and a year as 360 days was originally devised for its ease of calculation by hand compared with the actual days between two dates. Because 360 is highly factorable, payment frequencies of semi-annual and quarterly and monthly will be 180, 90, and 30 days of a 360 day year, meaning the payment amount will not change between payment periods.

The Actual/360 method calls for the borrower for the actual number of days in a month. This effectively means that the borrower is paying interest for 5 or 6 additional days a year as compared to the 30/360 day count convention. Spreads and rates on Actual/360 transactions are typically lower, e.g., 9 basis points. Since monthly loan payments are the same for both methods and since the investor is being paid for an additional 5 or 6 days of interest with the Actual/360 year base, the loan’s principal is reduced at a slightly lower rate. This leaves the loan balance 1-2% higher than a 30/360 10-year loan with the same payment.

Business date convention

Date rolling (business date) conventions are a common practice to adjust non-business days into business days.

Footnotes

1. ↑ "Investopedia definition". investopedia.com. 
2. ↑ see the treatment of 30/360 in (Mayle 1993).
3. ↑ the ISDA 2006 vs. ISDA 2000 definitions, for instance.
4. ↑ 4.0 4.1 4.2 4.3 4.4 "EMU and Market Conventions: Recent Developments". 1998. Retrieved 2014-09-18. 
5. ↑ "Practical Issues Arising from the Introduction of the Euro - Issue 7". 12 March 1998. Retrieved 2014-09-18. 
6. ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 6.8 "ISDA Definitions, Section 4.16". 2006. Retrieved 2014-09-18. 
7. ↑ 7.0 7.1 7.2 7.3 "ICMA Rule Book, Rule 251". Retrieved 2014-09-18. 
8. ↑ 8.0 8.1 "Bulletin Officiel d la Banque de France, Définitions communes a plusieurs additifs techniques". January 1999. Retrieved 2014-09-18.  |chapter= ignored (help)
9. ↑ 9.0 9.1 "FBF Master Agreement for Financial Transactions, Supplement to the Derivatives Annex, Edition 2004". 2004. Retrieved 2014-09-18. 

References

• Mayle, Jan (1993), Standard Securities Calculation Methods: Fixed Income Securities Formulas for Price, Yield and Accrued Interest 1 (3rd ed.), Securities Industry and Financial Markets Association, ISBN 1-882936-01-9 . The standard reference for conventions applicable to US securities. For the 30/360 US convention, this edition adds the first two rules to those given in earlier editions.

• ICMA Rule Book, Rule 251, retrieved 2007-07-31 . ICMA's definition of certain day count conventions.

• ISDA Definitions, Section 4.16, 2006 . ISDA's definition of certain day count conventions. Note that these definitions differ in some cases from the ISDA's Annex to the 2000 Definitions.

• EMU and Market Conventions: Recent Developments, 1998, retrieved 2007-07-31 . ISDA's discussion of market convergence, including an extensive discussion of irregular coupon periods.

• FBF Master Agreement for Financial Transactions, Supplement to the Derivatives Annex, Edition 2004, 2004, retrieved 2014-09-13 . Definition of various day counts in section 7.

Further reading

• Financial Interest Calculator. Online calculation of interest with different day count conventions, created by eTradeTech.com.
• Bond Calculator. Online calculation of interest and rate indicators with different day count conventions, created by SIX Swiss Exchange.
• Pricing of Game Options (in a market with stochastic interest rates) - Section Chapter II: A Little Bit of Finance, Section 1: Brief introduction to Financial Securities, from pages 26 to 33, formally mention day count conventions.
• Practical Issues Arising from the Introduction of the Euro - Issue 7 (March 1998) - Chapter 4: Financial Markets and Exchanges: discusses European nations' day-count conventions and changes required to unify the day-count conventions for the EU member states.
• jFin pure Java open source implementation of financial date arithmetic.
• comparison of financial day count convention used in Excel and OOXML
• Interest Rate Instruments and Market Conventions Guide. A reference guide containing conventions and market standards for the most common financial instruments.
• Day Count Conventions, 2007, retrieved 2007-07-31 . Web page on the history and context of day count conventions, including a cross-reference.
• Online Day Count Calculator. Online Day Count Calculator for Common Conventions

Related information

Bond market Bond Debenture Fixed income Types of bonds by issuer Agency bond Corporate bond Senior debt Subordinated debt Distressed debt Emerging market debt Government bond Municipal bond Types of bonds by payout Accrual bond Auction rate security Callable bond Commercial paper Convertible bond Exchangeable bond Extendible bond Fixed rate bond Floating rate note High-yield debt Inflation-indexed bond Inverse floating rate note Perpetual bond Puttable bond Reverse convertible securities Zero-coupon bond Bond valuation Clean price Convexity Coupon Credit spread Current yield Dirty price Duration I-spread Mortgage yield Nominal yield Yield to maturity Z-spread Securitized products Asset-backed security Collateralized debt obligation Collateralized mortgage obligation Commercial mortgage-backed security Mortgage-backed security Yield-curve spread Bond options Callable bond Convertible bond Embedded option Exchangeable bond Extendible bond Option-adjusted spread Puttable bond Institutions Commercial Mortgage Securities Association (CMSA) International Capital Market Association (ICMA) Securities Industry and Financial Markets Association (SIFMA)