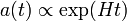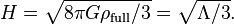Dark-energy-dominated era

In physical cosmology, the dark-energy-dominated era refers to the last of the three phases of the known universe, the other two being the matter-dominated era and the radiation-dominated era. The dark-energy-dominated era began after the matter-dominated era, i.e. when the Universe was about 9.8 billion years old.[1] As other forms of the matter – dust and radiation – dropped to very low concentrations, the cosmological constant term started to dominate the energy density of the Universe.

For a dark-energy-dominated universe, the evolution of the scale factor in the Friedmann–Lemaître–Robertson–Walker metric is easily obtained solving the Friedmann equations:

a(t)\propto \exp(Ht)

Here, the coefficient H in the exponential, the Hubble constant, is

H = \sqrt{8\pi G \rho_\mathrm{full} / 3} = \sqrt{\Lambda / 3}.

This exponential dependence on time makes the spacetime geometry identical to the de Sitter Universe, and only holds for a positive sign of the cosmological constant, the sign that was observed to be realized in Nature anyway. The current density of the observable universe is of the order of 9.44 x 10−27kg m−3 and the age of the universe is of the order of 13.8 billion years, or 4.358 x 1017s. The Hubble parameter, H, is ~70.88 km s−1Mpc−1. (The Hubble time is 13.79 billion years.) The value of the cosmological constant, Λ, is ~2 x 10−35s−2.

See also

References

  1. ↑ Ryden, Barbara, "Introduction to Cosmology", 2006, eqn. 6.33