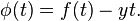Darboux's theorem (analysis)
Darboux's theorem is a theorem in real analysis, named after Jean Gaston Darboux. It states that all functions that result from the differentiation of other functions have the intermediate value property: the image of an interval is also an interval.
When f is continuously differentiable (f in C1([a,b])), this is a consequence of the intermediate value theorem. But even when f′ is not continuous, Darboux's theorem places a severe restriction on what it can be.
Darboux's theorem
Let 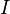 be an open interval,
be an open interval, 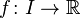 a real-valued differentiable function. Then
a real-valued differentiable function. Then 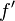 has the intermediate value property: If
has the intermediate value property: If  and
and  are points in
are points in 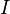 with
with 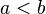 , then for every
, then for every  between
between  and
and 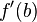 , there exists an
, there exists an  in
in ![[a,b]](../I/m/2c3d331bc98b44e71cb2aae9edadca7e.png) such that
such that 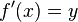 .[1]
.[1]
Proof
If  equals
equals  or
or 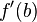 , then setting
, then setting  equal to
equal to  or
or  , respectively, works. Therefore, without loss of generality, we may assume that
, respectively, works. Therefore, without loss of generality, we may assume that  is strictly between
is strictly between  and
and 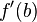 , and in particular that
, and in particular that 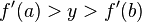 . Define a new function
. Define a new function 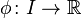 by
by
Since  is continuous on the closed interval
is continuous on the closed interval ![[a,b]](../I/m/2c3d331bc98b44e71cb2aae9edadca7e.png) , its maximum value on that interval is attained, according to the extreme value theorem, at a point
, its maximum value on that interval is attained, according to the extreme value theorem, at a point  in that interval, i.e. at some
in that interval, i.e. at some ![x\in[a,b]](../I/m/8290bddba5acf9822dcbf61f4ac67d1b.png) . Because
. Because 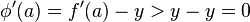 and
and 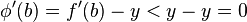 , Fermat's theorem implies that neither
, Fermat's theorem implies that neither  nor
nor  can be a point, such as
can be a point, such as  , at which
, at which  attains a local maximum. Therefore,
attains a local maximum. Therefore, 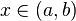 . Hence, again by Fermat's theorem,
. Hence, again by Fermat's theorem, 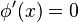 , i.e.
, i.e. 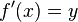 .[1]
.[1]
Another proof based solely on the mean value theorem and the intermediate value theorem is due to Lars Olsen.[1]
Darboux function
A Darboux function is a real-valued function f which has the "intermediate value property": for any two values a and b in the domain of f, and any y between f(a) and f(b), there is some c between a and b with f(c) = y.[2] By the intermediate value theorem, every continuous function is a Darboux function. Darboux's contribution was to show that there are discontinuous Darboux functions.
Every discontinuity of a Darboux function is essential, that is, at any point of discontinuity, at least one of the left hand and right hand limits does not exist.
An example of a Darboux function that is discontinuous at one point, is the function 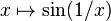 .
.
By Darboux's theorem, the derivative of any differentiable function is a Darboux function. In particular, the derivative of the function 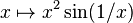 is a Darboux function that is not continuous.
is a Darboux function that is not continuous.
An example of a Darboux function that is nowhere continuous is the Conway base 13 function.
Darboux functions are a quite general class of functions. It turns out that any real-valued function f on the real line can be written as the sum of two Darboux functions.[3] This implies in particular that the class of Darboux functions is not closed under addition.
A strongly Darboux function is one for which the image of every (non-empty) open interval is the whole real line. Such functions exist and are Darboux but nowhere continuous.[2]
Notes
- ↑ 1.0 1.1 1.2 Olsen, Lars: A New Proof of Darboux's Theorem, Vol. 111, No. 8 (Oct., 2004) (pp. 713–715), The American Mathematical Monthly
- ↑ 2.0 2.1 Ciesielski, Krzysztof (1997). Set theory for the working mathematician. London Mathematical Society Student Texts 39. Cambridge: Cambridge University Press. pp. 106–111. ISBN 0-521-59441-3. Zbl 0938.03067.
- ↑ Bruckner, Andrew M: Differentiation of real functions, 2 ed, page 6, American Mathematical Society, 1994
External links
- This article incorporates material from Darboux's theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
- Hazewinkel, Michiel, ed. (2001), "Darboux theorem", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4