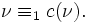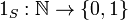Cylindric numbering

In computability theory a cylindric numbering is a special kind of numbering first introduced by Yuri L. Ershov in 1973.

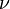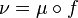If a numberings $\nu$ is reducible to $\mu$ then there exists a computable function $f$ with $\nu = \mu \circ f$ . Usually $f$ is not injective but if $\mu$ is a cylindric numbering we can always find an injective $f$ .

Definition

A numbering 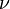$\nu$ is called cylindric if

\nu \equiv_1 c(\nu).

That is if it is one-equivalent to its cylindrification

A set $S$ is called cylindric if its indicator function

1_S: \mathbb{N} \to \{0,1\}

is a cylindric numbering.

Examples

every Gödel numbering is cylindric

Properties

cylindric numberings are idempotent, $\nu \circ \nu = \nu$

References

Yu. L. Ershov, "Theorie der Numerierungen I." Zeitschrift für mathematische Logik und Grundlagen der Mathematik 19, 289-388 (1973).