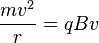Cyclotron resonance

Cyclotron resonance describes the interaction of external forces with charged particles experiencing a magnetic field, thus already moving on a circular path. It is named after the cyclotron, a cyclic particle accelerator that utilizes an oscillating electric field tuned to this resonance to add kinetic energy to charged particles.

The cyclotron frequency or gyrofrequency is the frequency of a charged particle moving perpendicular to the direction of a uniform magnetic field B (constant magnitude and direction). Since that motion is always circular,^[1] the cyclotron frequency is given by equality of centripetal force and magnetic Lorentz force

\frac{mv^2}{r} = qBv

with the particle mass m, its charge q, velocity v, and the circular path radius r, also called gyroradius.

By substitution for the circulation frequency 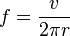$f = \frac{v}{2 \pi r}$ which defines the cyclotron frequency, this leads to

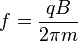f = \frac{q B}{2\pi m}

or the angular frequency

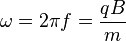\omega = 2 \pi f = \frac{q B}{m}

It is notable that the cyclotron frequency is independent of the radius and velocity and therefore independent of the particle's energy.

References

↑ Physics by M. Alonso & E. Finn, Addison Wesley 1996.

Cyclotron resonance

See also

References