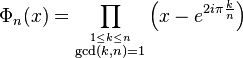Cyclotomic field

In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to $Q$ , the field of rational numbers. The $n$ -th cyclotomic field $Q (ζ n)$ (where $n > 2$ ) is obtained by adjoining a primitive $n$ -th root of unity $ζ n$ to the rational numbers.

The cyclotomic fields played a crucial role in the development of modern algebra and number theory because of their relation with Fermat's last theorem. It was in the process of his deep investigations of the arithmetic of these fields (for prime $n$ ) – and more precisely, because of the failure of unique factorization in their rings of integers – that Ernst Kummer first introduced the concept of an ideal number and proved his celebrated congruences.

Properties

A cyclotomic field is the splitting field of the cyclotomic polynomial

\Phi_n(x) = \prod_\stackrel{1\le k\le n}{\gcd(k,n)=1} \left(x-e^{2i\pi\frac{k}{n}}\right)

and therefore it is a Galois extension of the field of rational numbers. The degree of the extension

[Q (ζ n): Q]

is given by $φ (n)$ where $φ$ is Euler's phi function. A complete set of Galois conjugates is given by ${ (ζ n) a}$ , where $a$ runs over the set of invertible residues modulo $n$ (so that $a$ is relative prime to $n$ ). The Galois group is naturally isomorphic to the multiplicative group

(Z / n Z) \times

of invertible residues modulo $n$ , and it acts on the primitive $n$ th roots of unity by the formula

b : (ζ n) a \to (ζ n) a b

Relation with regular polygons

Gauss made early inroads in the theory of cyclotomic fields, in connection with the geometrical problem of constructing a regular $n$ -gon with a compass and straightedge. His surprising result that had escaped his predecessors was that a regular heptadecagon (with 17 sides) could be so constructed. More generally, if $p$ is a prime number, then a regular $p$ -gon can be constructed if and only if $p$ is a Fermat prime; in other words if $\varphi(p)=2^k$ is a power of 2.

For $n = 3$ and $n = 6$ primitive roots of unity admit a simple expression via square root of three, namely:

ζ 3 =

√3

i

− 1/2,

ζ 6 =

√3

i

+ 1/2

Hence, both corresponding cyclotomic fields are identical to the quadratic field Q(√−3). In the case of $ζ 4 = i =$ √−1 the identity of $Q (ζ 4)$ to a quadratic field is even more obvious. This is not the case for $n = 5$ though, because expressing roots of unity requires square roots of quadratic integers, that means that roots belong to a second iteration of quadratic extension. The geometric problem for a general $n$ can be reduced to the following question in Galois theory: can the $n$ th cyclotomic field be built as a sequence of quadratic extensions?

Relation with Fermat's Last Theorem

A natural approach to proving Fermat's Last Theorem is to factor the binomial $x n + y n$ , where $n$ is an odd prime, appearing in one side of Fermat's equation

x n + y n = z n

as follows:

x n + y n = (x + y) (x + ζ y) \dots (x + ζ n - 1 y)

Here $x$ and $y$ are ordinary integers, whereas the factors are algebraic integers in the cyclotomic field $Q (ζ n)$ . If unique factorization of algebraic integers were true, then it could have been used to rule out the existence of nontrivial solutions to Fermat's equation.

Several attempts to tackle Fermat's Last Theorem proceeded along these lines, and both Fermat's proof for $n = 4$ and Euler's proof for $n = 3$ can be recast in these terms. Unfortunately, the unique factorization fails in general – for example, for $n = 23$ – but Kummer found a way around this difficulty. He introduced a replacement for the prime numbers in the cyclotomic field $Q (ζ p)$ , expressed the failure of unique factorization quantitatively via the class number $h p$ and proved that if $h p$ is not divisible by $p$ (such numbers $p$ are called regular primes) then Fermat's theorem is true for the exponent $n = p$ . Furthermore, he gave a criterion to determine which primes are regular and using it, established Fermat's theorem for all prime exponents $p$ less than 100, with the exception of the irregular primes 37, 59, and 67. Kummer's work on the congruences for the class numbers of cyclotomic fields was generalized in the twentieth century by Iwasawa in Iwasawa theory and by Kubota and Leopoldt in their theory of p-adic zeta functions.

List of Class Numbers to Cyclotomic Field

(sequence A061653 in OEIS), or A055513 (for prime n)

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Class number	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
n	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
Class number	1	1	3	1	1	1	1	1	8	1	9	1	1	1	1	1	37	1	2	1
n	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
Class number	121	1	211	1	1	3	695	1	43	1	5	3	4889	1	10	2	9	8	41241	1
n	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80
Class number	76301	9	7	17	64	1	853513	8	69	1	3882809	3	11957417	37	11	19	1280	2	100146415	5
n	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100
Class number	2593	121	838216959	1	6205	211	1536	55	13379363737	1	53872	201	6795	695	107692	9	411322824001	43	2883	55
n	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120
Class number	3547404378125	5	9069094643165	351	13	4889	63434933542623	19	161784800122409	10	480852	468	1612072001362952	9	44697909	10752	132678	41241	1238459625	4
n	121	122	123	124	125	126	127	128	129	130	131	132	133	134	135	136	137	138	139	140
Class number	12188792628211	76301	8425472	75456	57708445601	7	2604529186263992195	359057	37821539	64	28496379729272136525	11	157577452812	853513	75961	111744	646901570175200968153	69	1753848916484925681747	39
n	141	142	143	144	145	146	147	148	149	150	151	152	153	154	155	156	157	158	159	160
Class number	1257700495	3882809	36027143124175	507	1467250393088	11957417	5874617	4827501	687887859687174720123201	11	2333546653547742584439257	1666737	2416282880	1280	84473643916800	156	56234327700401832767069245	100146415	223233182255	31365

References

Bryan Birch, "Cyclotomic fields and Kummer extensions", in J.W.S. Cassels and A. Frohlich (edd), Algebraic number theory, Academic Press, 1973. Chap.III, pp. 45–93.
Daniel A. Marcus, Number Fields, third edition, Springer-Verlag, 1977
Lawrence C. Washington, Introduction to Cyclotomic Fields, Graduate Texts in Mathematics, 83. Springer-Verlag, New York, 1982. ISBN 0-387-90622-3
Serge Lang, Cyclotomic Fields I and II, Combined second edition. With an appendix by Karl Rubin. Graduate Texts in Mathematics, 121. Springer-Verlag, New York, 1990. ISBN 0-387-96671-4