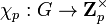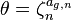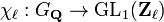Cyclotomic character
In number theory, a cyclotomic character is a character of a Galois group giving the Galois action on a group of roots of unity. As a one-dimensional representation over a ring R, its representation space is generally denoted by R(1) (that is, it is a representation χ : G → AutR(R(1)) ≈ GL(1, R)).
p-adic cyclotomic character
If p is a prime, and G is the absolute Galois group of the rational numbers, the p-adic cyclotomic character is a group homomorphism
where Zp× is the group of units of the ring of p-adic integers. This homomorphism is defined as follows. Let ζn be a primitive pn root of unity. Every pn root of unity is a power of ζn uniquely defined as an element of the ring of integers modulo pn. Primitive roots of unity correspond to the invertible elements, i.e. to (Z/pn)×. An element g of the Galois group G sends ζn to another primitive pn root of unity
where ag,n ∈ (Z/pn)×. For a given g, as n varies, the ag,n form a comptatible system in the sense that they give an element of the inverse limit of the (Z/pn)×, which is Zp×. Therefore, the p-adic cyclotomic character sends g to the system (ag,n)n, thus encoding the action of g on all p-power roots of unity.
In fact, 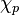 is a continuous homomorphism (where the topology on G is the Krull topology, and that on Zp× is the p-adic topology).
is a continuous homomorphism (where the topology on G is the Krull topology, and that on Zp× is the p-adic topology).
As a compatible system of ℓ-adic representations
By varying ℓ over all prime numbers, a compatible system of ℓ-adic representations is obtained from the ℓ-adic cyclotomic characters (when considering compatible systems of representations, the standard terminology is to use the symbol ℓ to denote a prime instead of p). That is to say, χ = { χℓ }ℓ is a "family" of ℓ-adic representations
satisfying certain compatibilities between different primes. In fact, the χℓ form a strictly compatible system of ℓ-adic representations.
Geometric realizations
The p-adic cyclotomic character is the p-adic Tate module of the multiplicative group scheme Gm,Q over Q. As such, its representation space can be viewed as the inverse limit of the groups of pnth roots of unity in Q.
In terms of cohomology, the p-adic cyclotomic character is the dual of the first p-adic étale cohomology group of Gm. It can also be found in the étale cohomology of a projective variety, namely the projective line: it is the dual of H2ét( P1 ).
In terms of motives, the p-adic cyclotomic character is the p-adic realization of the Tate motive Z(1). As a Grothendieck motive, the Tate motive is the dual of H2( P1 ).[1]
Properties
The p-adic cyclotomic character satisfies several nice properties.
- It is unramified at all primes ℓ ≠ p (i.e. the inertia subgroup at ℓ acts trivially).
- If Frobℓ is a Frobenius element for ℓ ≠ p, then χp(Frobℓ) = ℓ
- It is crystalline at p.
See also
References
- ↑ Section 3 of Deligne, Pierre (1979), "Valeurs de fonctions L et périodes d'intégrales", in Borel, Armand; Casselman, William, Automorphic Forms, Representations, and L-Functions, Proceedings of the Symposium in Pure Mathematics (in French) 33.2, Providence, RI: AMS, p. 325, ISBN 0-8218-1437-0, MR 0546622, Zbl 0449.10022