Cyclohedron
Cyclohedron W3
In geometry, the cyclohedron or Bott–Taubes polytope is a certain (n − 1)-dimensional polytope that is useful in studying knot invariants.[1]
The configuration space of n distinct points on the circle S1 is an n-dimensional manifold, which can be compactified into a manifold with corners by allowing the points to approach each other. This compactification can be factored as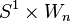 
, where Wn is the cyclohedron.
See also
Notes
- ↑ Stasheff 1997, p. 58.
References
- Stasheff, Jim (1997), "From operads to 'physically' inspired theories", in Loday, Jean-Louis; Stasheff, James D.; Voronov, Alexander A., Operads: Proceedings of Renaissance Conferences, Contemporary Mathematics 202, AMS Bookstore, pp. 53–82, ISBN 978-0-8218-0513-8, retrieved 1 May 2011
Further reading
- Forcey, Stefan; Springfield, Derriell (December 2010), "Geometric combinatorial algebras: cyclohedron and simplex", Journal of Algebraic Combinatorics 32 (4): 597–627, arXiv:0908.3111, doi:10.1007/s10801-010-0229-5
- Morton, James; Pachter, Lior; Shiu, Anne; Sturmfels, Bernd (January 2007), "The Cyclohedron Test for Finding Periodic Genes in Time Course Expression Studies", Statistical Applications in Genetics and Molecular Biology 6 (1), arXiv:q-bio/0702049, doi:10.2202/1544-6115.1286
External links
- Bryan Jacobs, "Cyclohedron", MathWorld.