Cycle decomposition (graph theory)

For the notation used to express permutations, see Cycle decomposition (group theory).

In graph theory, a cycle decomposition is a partitioning of the edges of a graph into subsets, such that the edges in each subset lie on a cycle.

Given a graph G separate this graph into proper subgraphs in such a way that no two subgraphs have a common edge and the union of these subgraphs will give us the original graph. We call the set of these subgraphs the decomposition of G.

A cycle decomposition is a decomposition such that each subgraph 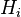H_i in the decomposition is a cycle. Every vertex in a graph that has a cycle decomposition must have even degree.

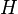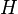H is a spanning subgraph of G, if H is obtained from graph G only by the removal of edges. Therefore, graph 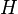H has all the vertices of graph G.

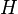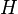A spanning subgraph H of a graph G is called an r-factor of G if H is regular of degree r. That is, all the vertices of 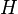H have the same degree, namely r.

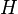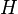A spanning subgraph H of graph G is called a 1-factor of G if H is regular of degree 1. Thus, no two edges of a 1-factor share a vertex and there are no isolated vertices. To have a 1-factor, a graph must have an even number of vertices. 1-factors are also called matchings.

Cycle decomposition of 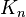K_n and K_n-I

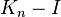
Brian Alspach and Heather Gavlas have established necessary and sufficient conditions for the existence of a decomposition of a complete graph of even order minus a 1-factor into even cycles and a complete graph of odd order into odd cycles.[1] Prior to this result the existence of cycle decompositions of a complete graph required the degree of the vertices to be even; therefore the complete graph must have an odd number of vertices. However, the authors were able to find a way to decompose a complete graph with an even number of vertices by removing a 1-factor. Their proof relies on Cayley graphs, in particular, circulant graphs. Also many of their decompositions come from the action of a permutation on a fixed subgraph.

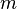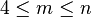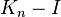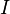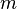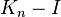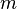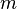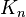They proved that for positive even integers m and n with 4\leq m\leq n ,the graph K_n-I (where I is a 1-factor) can be decomposed into cycles of length m if and only if the number of edges in K_n-I is a multiple of m. Also, for positive odd integers m and n with 3≤m≤n, the graph K_n can be decomposed into cycles of length m if and only if the number of edges in 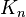K_n is a multiple of m.

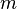References

  1. ↑ Science Direct Article