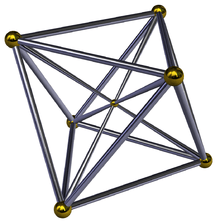
Cubic pyramid
| Cubic pyramid | ||
|---|---|---|
 Schlegel diagram | ||
| Type | Polyhedral pyramid | |
| Schläfli symbol | ( ) ∨ {4,3} ( ) ∨ [{4} × { }] ( ) ∨ [{ } × { } × { }] | |
| Cells | 7 | 1 cube 6 square pyramids |
| Faces | 18 | 12 {3} 6 {4} |
| Edges | 20 | |
| Vertices | 9 | |
| Dual | Octahedral pyramid | |
| Symmetry group | B3, [4,3,1], order 48 [4,2,1], order 16 [2,2,1], order 8 | |
| Properties | convex, regular-faced | |
In 4-dimensional geometry, the cubic pyramid is bounded by one cube on the base and 6 square pyramid cells which meet at the apex. Since a cube has a circumradius divided by edge length less than one,[1] the square pyramids can made with regular faces by computing the appropriate height.
The regular 24-cell has cubic pyramids around every vertex.
The dual to the cubic pyramid is a octahedral pyramid, seen as an octahedral base, and 8 regular tetrahedral meeting at an apex.
Related polytopes and honeycombs
A cubic pyramid of height zero can be seen as a cube divided into 6 square pyramids along with the center point. These square pyramid-filled cubes can tessellate three-dimensional space as a dual of the truncated cubic honeycomb, called a hexakis cubic honeycomb, or pyramidille.
References
- ↑ Richard Klitzing, 3D convex uniform polyhedra, o3o4x - cube sqrt(3)/2 = 0.866025
External links
- Olshevsky, George, Pyramid at Glossary for Hyperspace.
- Richard Klitzing, 4D, Segmentotopes Richard Klitzing, Segmentotope, cubpy, K-4.26
- Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra
| Wikimedia Commons has media related to Pyramids (geometry). |