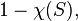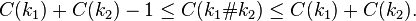Crosscap number

In the mathematical field of knot theory, the crosscap number of a knot K is the minimum of

taken over all compact, connected, non-orientable surfaces S bounding K; here 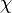is the Euler characteristic. The crosscap number of the unknot is zero, as the Euler characteristic of the disk is one.

Examples

• The crosscap number of the trefoil knot is 1, as it bounds a Möbius strip and is not trivial.
• The crosscap number of a torus knot was determined by M. Teragaito.

The formula for the knot sum is

Further reading

• Clark, B.E. "Crosscaps and Knots", Int. J. Math and Math. Sci, Vol 1, 1978, pp 113–124
• Murakami, Hitoshi and Yasuhara, Akira. "Crosscap number of a knot," Pacific J. Math. 171 (1995), no. 1, 261–273.
• Teragaito, Masakazu. "Crosscap numbers of torus knots," Topology Appl. 138 (2004), no. 1–3, 219–238.
• Teragaito, Masakazu and Hirasawa, Mikami. "Crosscap numbers of 2-bridge knots," Arxiv:math.GT/0504446.
• J.Uhing. "Zur Kreuzhaubenzahl von Knoten", diploma thesis, 1997, University of Dortmund, (German language)

External links

• "Crosscap Number", KnotInfo.