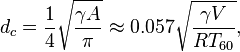Critical distance

For the ethological term, see Critical distance (animals).

Critical distance is, in audio physics, the distance at which the sound pressure level of the direct sound D and the reverberant sound R are equal when dealing with a directional source. In other words, the point in space where the combined amplitude of all the reflected echoes are the same as the amplitude of the sound coming directly from the source (D = R). This distance, called the critical distance 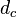$d_c$ , is dependent on the geometry and absorption of the space in which the sound waves propagate, as well as the dimensions and shape of the sound source.

In a reverberant space, the sound perceived by a listener is a combination of direct and reverberant sound. The ratio of direct sound is dependent on the distance between the source and the listener, and upon the reverberation time in [the room]. At a certain distance the two will be equal. This is called the "critical distance."
—Glenn White and Gary Louie (2005)^[1]

A reverberant room generates a short critical distance and an acoustically dead (anechoic) room generates a longer critical distance.

Calculation

The calculation of the critical distance for a diffuse approximation of the reverberant field:

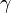d_c = \frac{1}{4} \sqrt \frac{\gamma A}{\pi} \approx 0.057 \sqrt \frac{\gamma V}{RT_{60}} ,

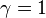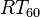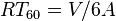where $\gamma$ is the degree of directivity of the source ( $\gamma = 1$ for an omnidirectional source), $A$ the equivalent absorption surface, $V$ the room volume in m³ and $RT_{60}$ the reverberation time of room in seconds. The latter approximation is using Sabine's reverberation formula $RT_{60}=V/6A$ .

Listen to this article (info/dl)

This audio file was created from a revision of the "Critical distance" article dated 2006-12-17, and does not reflect subsequent edits to the article. (Audio help)

More spoken articles

Sources

↑ White, Glenn and Louie, Gary (2005). The Audio Dictionary, 3rd edition, p.89. University of Washington Press. Cited in Hodgson, Jay (2010). Understanding Records, p.36. ISBN 978-1-4411-5607-5.

Music production

Techniques

Engineering	Audio filter Audio mastering Audio mixing Critical distance Effects loop Diffusion Overdubbing Punch in/out

Post-processing	Pitch shift Auto-Tune Chorus effect Compression Delay effect (STEED) Distortion Double tracking (ADT) Ducking Equalization Exciter effect Farkle effect Flanging Octave effect Noise gate Phaser Pumping Reverberation Reverse echo

Formulas

Luminaries

Other