Credit rationing
Credit rationing refers to the situation where lenders limit the supply of additional credit to borrowers who demand funds, even if the latter are willing to pay higher interest rates. It is an example of market imperfection, or market failure, as the price mechanism fails to bring about equilibrium in the market. It should not be confused with cases where credit is simply "too expensive" for some borrowers, that is, situations where the interest rate is deemed too high. On the contrary, the borrower would like to acquire the funds at the current rates, and the imperfection refers to the absence of equilibrium in spite of willing borrowers. In other words, at the prevailing market interest rate, demand exceeds supply, but lenders are not willing to either loan more funds, or raise the interest rate charged, as they are already maximising profits.[1]
Credit rationing is not the same phenomenon as the better-known case of food rationing, common in times of war. In that case, shortages lead governments to control the food portions allocated to individuals, who would be willing to pay higher prices for more portions. However, credit rationing is not necessarily the result of credit shortages but rather of asymmetric information. More importantly, food rationing is a result of direct government action, while credit rationing is a market outcome.
Two main types of credit rationing can usually be distinguished. "Redlining" refers to the situation where some specific group of borrowers, who share an identifiable trait, cannot obtain credit with a given supply of loanable funds, but could if the supply were increased. More importantly, they would not be able to get loans even if they were willing to pay higher interest rates. "Pure credit rationing" refers to the situation where, within an observationally indistinguishable group, some obtain credit, while others do not, and will not receive credit even if they are willing to pay a higher interest rate.[2] A third and less interesting type is disequilibrium credit rationing, which is a temporary feature of the market, due to some friction preventing clearing.
Theoretical background
One of the main roles markets play is allocational; they allocate goods to the buyers with the highest valuation. Market equilibrium occurs when the demand of a good at the equilibrium price is equal to the supply of the good. If prices are deemed "too high" by the consumers, supply will exceed demand, and sellers will have to reduce their prices until the market clears (i.e. equilibrium is reached). On the other hand, if prices are "too low", then demand will be higher than supply, and prices will have to be raised to obtain market clearing.
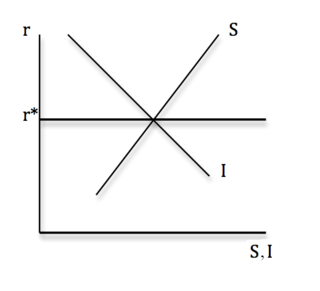
The graph to the right shows this simplified case for the credit market, and is usually referred to as the loanable funds model.[3] The interest rate is denoted by r, and S and I denote savings and investment respectively. This is a highly stylised example, where one abstracts from changes in output, and where the economy is in financial autarky (and, consequently, savings and investment express the supply and demand of loanable funds, respectively).
Equilibrium will be attained at the point where S=I, at the equilibrium interest rate r*. At r>r*, credit is "too expensive", as the interest rate is effectively the price of credit, and there is a resulting excess supply of credit. The interest rate will have to fall in order to clear the market.
Disequilibrium credit rationing
The more mundane case of credit rationing occurs when the credit market is, for one reason or another, out of equilibrium. This could be either because of some friction in the market, or some government policy (such as anti-usury laws), which prevent supply and demand from being equalised.[4] This has hardly a precise definition, but one should think of disequilibrium outcomes as temporary adjustments to shocks as the economy moves back to the long run equilibrium i.e. the equilibrium that will attain over some indeterminate amount of time in the absence of more external shocks. The main distinguishing factor between equilibrium and disequilibrium rationing in the credit markets is that the latter is not a long term feature, and can be alleviated through changes in policy or simply through time, and does not necessarily reflect chronic or structural features of the credit market. The most important contribution in this vein was by Dwight Jaffee and Franco Modigliani,[5] who first introduced this idea within a supply and demand framework.
The more interesting case, that of equilibrium credit rationing, is the result of structural features of the market (in particular, adverse selection), and will characterise long run market outcomes (barring some technological breakthrough), and is analysed below.
Equilibrium credit rationing - Stiglitz and Weiss
The seminal theoretical contribution to the literature is that of Joseph Stiglitz and Andrew Weiss,[6] who studied credit rationing in market with imperfect information, in their namesake 1981 paper in the American Economic Review. Stiglitz and Weiss developed a model to illustrate how credit rationing can be an equilibrium feature of the market, in the sense that the rationed borrower would be willing to obtain the funds at an interest rate higher than the one charged by the lender, who will not be willing to lend the extra funds, as the higher rate would imply lower expected profits. It is equilibrium rationing as there exists excess demand for credit at the equilibrium rate of interest. The reason for that is adverse selection, the situation where the lender is faced with borrowers whose projects imply different risk levels (types), and the type of each borrower is unbeknownst to the lender. The main intuition behind this result is that safe borrowers would not be willing to tolerate a high interest rate, as, with a low probability of default, they will end up paying back a large amount to the lender. Risky types will accept a higher rate because they have a lower chance of a successful project (and typically a higher return if successful), and thus a lower chance of repayment. Note that this assumes limited liability, though results could still hold with unlimited liability.
Pure credit rationing
In a framework similar to Stiglitz and Weiss, one can imagine a group of individuals, prospective borrowers, who want to borrow funds in order to finance a project, which yields uncertain returns. Let there be two types of individuals, who are observationally identical, and only differ in the riskiness of their projects. Assume type A individuals are low risk compared to type B, in the sense that the expected return on type B projects is a mean preserving spread of type A projects; they have the same expected return, but higher variance.
For example, imagine that type A returns are uniformly distributed (meaning that all possible values have the same probability of occurring) from $75 to $125, so that the value of type A projects is at least $75 and at most $125, and the expected value (mean) is $100.
Now, assume type B project returns are also uniformly distributed, but their range is from $50 to $150. Type B project returns also have an expected value of $100, but are more risky.
Now assume that the bank knows that two types exist, and even knows what fraction of the potential borrowers applying for loans belong to each group, but cannot tell whether an individual applicant is type A or B. The implication to the bank of the difference in the riskiness of these projects is that each borrower has a different probability of repaying the loan, and this affects the bank's expected return. The bank would thus like to be able to identify (screen) the borrower types, and in the absence of other instruments to do so, it will use the interest rate.
This was the main intuitive observation of Stiglitz and Weiss. They realised that an individual that is willing to accept a higher interest rate in her loan is doing so because she knows that the riskiness of her project is such that there is lower probability of repaying the loan. In a limited liability setting, where the personal assets of the borrower might not be taken as collateral, the borrower might not object to paying a high enough interest rate, as she knows that the probability of the project succeeding is low, so probability of repayment is low. Even if the project does succeed, the returns will be high enough for a profit to be left after repaying the loan.[7] The safe borrowers have a high probability of repaying their loan, so even a modest interest rate, relative to their expected return, is likely to result in an unprofitable contract.
What this implies for the banks is that there will be a range of relatively low interest rates below which all the applicants will accept the loan, and a cut off point above which the safe borrowers decide to drop, as expected repayment becomes too high. In fact, as interest rates rise, the critical value of the project (think of it as expected return), above which the borrower is willing to borrow the money, also rises. Naturally, there exists a (higher) cut off point for the risky types as well, above which even they would not be willing to borrow.
This situation should show that the interest rate has two effects on banks' expected return. On the one hand, higher interest rates imply that, for a given loan, the repayment (if it does take place) will be higher, and this increases bank profits; this is the direct effect. On the other hand, and crucially for credit rationing, a higher interest rate might mean that the safe types are not anymore willing to accept the loans, and drop out of the market; this is the adverse selection effect.
These two effects together give an odd shape to the bank's expected return. It is strictly rising with the interest rate when the latter is low enough; at the point where the safe types drop out of the market (call it r1), expected return falls sharply, and then rises again, until the point where the risky types drop out as well (r2), falling to zero, as no one is accepting loans. Technically speaking, the expected return is non-monotonic in the interest rate, as it rising, then falling sharply, then rising again until it falls sharply to zero.
It follows then that if the level of the interest rate that maximises the bank's expected return is lower than the level after which risky types drop out, there might be credit rationing, if the supply of funds is low enough. If the optimal rate (from the point of view of the bank) is between r1 and r2, then only some of the risky types will be rationed (the safe types are unwilling to borrow at such a rate); they will not be given credit even at higher rates. If the optimal rate is below r1, then borrowers of both types will be rationed.
It might be more intuitive to imagine a situation with a very large number of types (continuum). In that case, the expected return function of the bank will become smooth, rising for low levels of the interest rate, until the optimal rate, and then falling smoothly until it reaches zero. Types that would be willing to borrow at rates higher than the optimal might be rationed.
It is important to note that as the supply of funds to the bank rises, some of the rationed people will get a loan, but at the same interest rate, which is still at the profit maximising level. For a sufficient rise in supply, everyone will receive loans, at which point the interest rate will have to fall.
Finally, if the optimal rate is high enough, we might have no rationing. This will happen if the level of the interest rate such that current supply of funds equal demand for funds is lower than the optimal rate, and equal to r1.[8] All the borrowers will receive funds at that rate.
Redlining
Redlining is a different situation, as it is not the result of adverse selection. In fact, the bank can perfectly distinguish between the different types of buyers according to some criterion. Each type is assumed to have a different expected return function (from the point of view of the bank).
As an illustration, consider the case of three types, 1, 2 and 3, which are ranked according to the maximum expected return they give to the bank, from lowest to highest. The maximum expected return a type 3 borrower can give to the bank (at the optimal interest rate for the borrower) is higher than that of type 2, which is higher than that of type 1.
For a sufficiently high cost of obtaining funds, only type 3 borrowers will receive credit. This will occur if the maximum expected return from type 2 borrowers is lower than that cost. If costs fall by enough, type 2 borrowers will obtain credit, and if they fall further so will type 1 borrowers. Every type that receives credit will be charged different interest rates, but the expected return to the bank will be equal for each type, as long as there is competition between banks.
It is important to note that type 1 borrowers obtain credit only if type 2 borrowers are not rationed, and so on.
This argument is quite pertinent in the context of the subprime mortgage crisis. Low interest rate setting by the Federal Reserve made the cost of loanable funds extremely low. On the other hand, the securitization practices of firms in the credit markets significantly raised the profitability of loans to people with poor credit ratings (type 1 in the example above), and thus contributed to massive leveraging of borrowers who would ordinarily have had a hard time receiving even modest loans.
Other contributions
The contribution of Stiglitz and Weiss was very crucial in addressing this important market outcome. It was one of a series of papers to address the important phenomenon of adverse selection in economics, pioneered by the classic study of the lemon problem in used car markets by George Akerlof,[9] and celebrated by the paper by Michael Rothschild and Stiglitz[10] on adverse selection in the insurance market. Many important studies followed their example, some with competing results, and extended the issue of credit rationing to further domains.
Before we go on discussing those studies, it is interesting to note that the first paper to treat credit rationing as a possible equilibrium phenomenon caused by adverse selection was by Dwight Jaffee and Thomas Russell in 1976.[11] In their model, low quality borrowers would like to "masquerade" as high quality in order to get lower rates, and a separating equilibrium (that is, with different contracts offered to the two types) entails lower rates, but also lower loans, for the high types. This approach did not become popular however, as the pooling equilibrium (both types offered the same contract), which implies credit rationing, is not sustainable; a pooling contract offered to both types that will be accepted by both types and give non-negative profits to the banks can be dominated (generate higher profits) by a contract with lower interest and loan amount, which will only be preferred by the high quality types, who will drop the pooling contract, making it unprofitable for the banks. So focus has shifted on applications that allow for stable equilibrium rationing.
Overinvestment
David De Meza and David C. Webb[12] argued the possibility that adverse selection could lead to the flip side of what Stiglitz and Weiss considered, namely over-investment. Their argument runs along the same lines as Akerlof's market for lemons. In this setting, prospective buyers of used cars do not know the quality of the car they are thinking of purchasing. Assuming they know the distribution of car quality across the market, they come to a maximum price they are willing to pay for the car. For example, suppose there are only two qualities, good and bad cars, worth $5000 and $1000 to the buyer respectively, but the buyer does not know the quality of the car she is about to buy. If she offers $5000, the sellers of either type surely accept, but the expected value of the car will only be equal to $3000 ($1000 with 50% probability and $5000 with 50% probability), so she will make expected losses of $2000. Hence, she will only be willing to pay $1000; only the bad car seller will accept, so the buyer will either end up with a bad car or with nothing. In this case, the adverse selection problem drives the good car out of the market. Extending this logic to more qualities, under certain conditions, the market might completely collapse.
Applying this framework to the market for credit, asymmetric information concerning the types of projects to be financed might lead to bad projects driving out good projects. De Meza and Webb's contribution is to show how the opposite might happen – that is, how good projects might draw in bad. Under some plausible conditions, the most crucial being that expected returns differ between different projects (whereas all projects in the Stiglitz and Weiss model have the same expected return but different levels of riskiness), they show that there cannot be a credit-rationing equilibrium. So the main difference here compared to Stiglitz and Weiss is that there is no specific level of the interest rate at which banks maximise profits – a small rise in interest rates if there is excess demand for credit will attract entrepreneurs and will not drive away existing borrowers.
As long as the supply of funds is increasing in the rate of return on deposits, there will be more investment compared to what the efficient solution would imply, that is, the level of investment that would take place if there were no asymmetry of information, and only the projects that should be financed are financed. The intuition is straightforward. If investment were lower than the efficient level, so would be the return on deposits. In addition, as less investment is taking place, the "worst" project that is financed must be better from the bank's point of view than the worst project that would be financed if investment were optimal. But if the bank is making a profit on the worst project that is financed, it will also be making profits on even worse projects (which were not financed before), leading to oversupply of credit and thus overinvestment.
Efficient credit rationing
When comparing their model to Stiglitz and Weiss, De Meza and Webb show that if credit rationing occurs in Stiglitz and Weiss, the volume of lending is actually higher than it would have been in the absence of rationing. This prompted a sister paper by the same authors,[13] where they show that, on the one hand, credit rationing can occur even under symmetric information, and, on the other, that it might not imply a market failure. This severely limits the scope of government intervention.
Moral hazard and credit rationing
Bengt Holmstrom and Jean Tirole (1998)[14] provide an example of credit rationing where asymmetric information does not lead to adverse selection, but instead moral hazard, the situation where deliberate actions by one of the parties of the contract, after the contract is signed, might affect outcomes. In their model, there are many entrepreneurs-borrower firms of only one type, who want to finance an investment opportunity, and have an initial level of assets that falls short of the amount needed for the investment. The twist in this model, compared to the cases described above, is that entrepreneurs can influence the outcome of the investment, by exerting high or low effort. High effort implies a high probability of a successful outcome, and low effort implies a lower one, but also gives a benefit to each borrower, in terms of higher leisure. So there is an incentive by borrowers not to exert high effort, even though doing so will result in higher probability of a successful outcome.
Competition between lenders and high effort by borrowers ensure positive outcomes for the society, so investment should take place. However, the fact that the lenders cannot observe the borrowers' behaviour implies that there is a minimum level of firm assets needed for banks to provide the loan. The firms will have to provide some of the project financing "out of their own pocket" and thus incur some of the investment risk. This will provide the bank with the necessary guarantee that the borrower has personal stakes in the success of the investment, and stands to make losses if it is unsuccessful, so that she will be interested in exerting high effort, making the bank willing to make the loan.
If a firm does not have the minimum amount of assets available (call it X), then its project will not be financed, and we will have credit rationing. This is the result of moral hazard, which creates what is termed in the literature as an agency cost, and can be thought of as arising from the benefit the borrower makes by exerting low effort. Higher agency cost and lower initial assets lead to more credit rationing.
Moral hazard in the subprime mortgage crisis
Moral hazard in credit markets was likely a major contributor to the subprime mortgage crisis and the ensuing credit crunch. In the context of this model, one can think of borrowers being real estate investors (or simply home owners investing in property) that used their current housing holdings as collateral assets when applying for loans. With rising house prices, and, more importantly, with the expectation of future rises in housing price, the expected return on the project to be financed was perceived to be higher than suggested by fundamentals, leading, on the one hand, to ever lower required X by banks in order to make loans, and, on the other, to inflated estimates of the value of the borrowers' initial assets. This led to less credit rationing, to the extent that good investments that should be undertaken got their financing, but also to subprime lending, where bad loans to poor projects were made. When the housing bubble burst, housing prices plummeted, so the expected return on projects fell, implying that banks needed very large initial assets holding, making lending scarcer and more difficult, resulting in a credit crunch. This provides a framework under which some credit rationing might be optimal, as a way of screening potentially harmful investments.
Credit rationing in sovereign lending
Finally, it is worthwhile to consider how credit rationing might arise as a feature of sovereign (government) lending, that is, lending to countries. Sovereign lending is a very different story than domestic lending, due to the absence of enforcement mechanisms in the case of bankruptcy, as there is no internationally acknowledged agency for such issues. If a country for one reason or another announces that it is either unable or unwilling to pay its debts, the most international lenders can do is renegotiate. Some experts believe that the threat of the country being shut off from financial markets if it defaults is not credible, as it has to be the case that absolutely no-one is willing to lend.[15] Others stress that though this might be true for the short trem, there are other reputational reasons why a country might want to avoid debt repudiation, mainly pertaining to the maintenance of good foreign relations, which allows access to international trade and technological innovations[16]
With these caveats, it is worthwhile to consider how reputation concerns can lead to credit rationing. The seminal contribution is by Jonathan Eaton and Mark Gersovitz,[17] who consider a simple model of international lending for a small open economy. Lenders set a maximum amount they are willing to lend (credit ceiling), which might be smaller or larger than the borrowing needs of the country. Countries face a penalty if they default, and whenever they are supposed to make debt payments, they consider whether they would be better off by defaulting, paying the penalty, and be forever barred from international credit markets, or pay the debt installment, borrowing again, and making the same decision next period.
As the probability of default is higher when debt is higher, there exists a level of lending that maximises expected return to the lender, and so the credit ceiling will depend on the probability of default. If desired lending is higher than the credit ceiling, some countries will not receive funds, and credit rationing will occur. This setting is reminiscent of Stiglitz and Weiss, as the interest rate has an incentive effect, and does not play the standard allocational role prices are supposed to play. As in that case, the allocation mechanism in Eaton and Gersovitz is credit rationing, which is not related to interest rate (the price of credit); at the going rate, countries want to borrow more but credit is denied.
Roy Harrod and the Effectiveness of Monetary Policy
Roy Harrod pointed to the existence of credit rationing early on. In his book Money he wrote that capital markets are highly imperfect and that in many markets there is no market price for certain customers. He argued that this was because these markets were characterized by negotiation processes that were liable to break down before a market price could be reached.
Harrod was also skeptical about the traditional transmission mechanism of monetary policy. Drawing on the famous Oxford surveys of businessmen in the 1930s he argued that it was likely that changes in the interest rate did not have a substantial effect on investment decisions. Harrod went on to argue that the main channel through which interest rates curtailed economic activity was through the process of what is now known as credit rationing. He wrote that: "It is essentially the imperfection of the capital market that makes monetary policy a powerful weapon." [18]
See also
Notes and References
- ↑ Definitions for the whole article are based on class notes by Anton Korinek, University of Maryland.
- ↑ Stiglitz, Joseph and Weiss, Andrew, Credit Rationing in Markets with Imperfect Information, The American Economic Review, Vol 71, No. 3 (June 1981), pp. 393-410.
- ↑ Krugman, Paul, May 2, 2009, New York Times website: http://krugman.blogs.nytimes.com/2009/05/02/liquidity-preference-loanable-funds-and-niall-ferguson-wonkish/.
- ↑ Leece, David, Economics of the mortgage market: perspectives on household decision making, London: Wiley-Blackwell, 2004, pp.94-96.
- ↑ Jaffee, Dwight M. and Modigliani, Franco, A Theory and Test of Credit Rationing, American Economic Review, 59 (1969), pp. 850–72.
- ↑ Stiglitz and Weiss, ibid.
- ↑ Note that the assumption is that the riskier project could lead to higher return than the safe project. The case where a project is more varied on a lower range (for example, uniform from $10 to $90, compared to $75 to $125) is theoretically uninteresting, as no profit maximising borrower (with conventionally risk averse preferences, or even mild preference for risk) would ever consider it.
- ↑ If there exist more than one equilibrium interest rates, then we are interested in the lowest one.
- ↑ Akerlof, George, The Market for Lemons: Qualitative Uncertainty and the Market Mechanism, Quarterly Journal of Economics, 84 (1970), pp 488-500.
- ↑ Rothschild, Michael and Stiglitz, Joseph, Equilibrium in Competitive Insurance Markets, Quarterly Journal of Economics, 91 (1976), pp. 629-649 .
- ↑ Jaffee, Dwight M. and Russell, Thomas, Imperfect Information, Uncertainty, and Credit Rationing, Quarterly Journal of Economics, 90 (1976), pp. 651–66
- ↑ De Meza, David, and Webb, David C., Too Much Investment: A Problem of Asymmetric Information, Quarterly Journal of Economics, 102 (1987), pp. 281–292
- ↑ De Meza, David, and Webb, David C., "Efficient Credit Rationing", European Economic Review, 102 (1992), pp. 1290 .
- ↑ Holmstrom, Bengt and Tirole, Jean, Private and Public Supply of Liquidity, Journal of Political Economy, 106 (1998), pages 1-40.
- ↑ Bullow, Jeremy and Rogoff, Kenneth, Sovereign Debt: Is to Forgive to Forget?, American Economic Review, 79 (1989), pp. 43-50.
- ↑ Cole, Harold L. and Kehoe, Patrick J., Reviving Reputation Models of International Debt, Federal Reserve Bank of Minneapolis Quarterly Review, Winter 1997.
- ↑ Eaton, Jonathan and Gersovitz, Mark, Debt With Potential Repudiation: Theoretical and Empirical Analysis, Review of Economic Studies, 48 (1981), pp. 435-445.
- ↑ Harrod, Roy, Money, Macmillan and Co, (1969), pp. 63-65.
See: Waller, Christopher and Stephen Lewarne, 'An Expository Model of Credit Rationing," Journal of Macroeconomics, Summer 1994, Vol. 16, No. 3, pp. 539-545