Credal set

A credal set is a set of probability distributions^[1] or, equivalently, a set of probability measures. A credal set is often assumed or constructed to be a closed convex set. It is intended to express uncertainty or doubt about the probability model that should be used, or to convey the beliefs of a Bayesian agent about the possible states of the world.^[2]

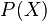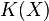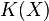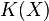Let $X$ denote a categorical variable, $P(X)$ a probability mass function over $X$ , and $K(X)$ a credal set over $X$ . If $K(X)$ is convex, the credal set can be equivalently described by its extreme points $\mathrm{ext}[K(X)]$ . The expectation for a function $f$ of $X$ with respect to the credal set $K(X)$ can be characterised only by its lower and upper bounds. For the lower bound,

\underline{E}[f]=\min_{P(X)\in K(X)} \sum_x f(x) P(x).

Notably, such an inference problem can be equivalently obtained by considering only the extreme points of the credal set.

It is easy to see that a credal set over a Boolean variable cannot have more than two vertices, while no bounds can be provided for credal sets over variables with three or more values.

References

↑ Levi, I. (1980). The Enterprise of Knowledge. MIT Press, Cambridge, Massachusetts.
↑ Cozman, F. (1999). Theory of Sets of Probabilities (and related models) in a Nutshell.

Credal set

See also

References

Further reading