Covering number
In mathematics, the idea of a covering number is to count how many small spherical balls would be needed to completely cover (with overlap) a given space. There are two closely related concepts as well, the packing number, which counts how many disjoint balls fit in a space, and the metric entropy, which counts how many points fit in a space when constrained to lie at some fixed minimum distance apart.
Mathematical Definition
More precisely, consider a subset  of a metric space
of a metric space 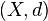 and a parameter
and a parameter 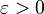 . Denote the ball of radius
. Denote the ball of radius  centered at the point
centered at the point 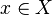 by
by 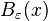 . There are two notions of covering number, internal and external, along with the packing number and the metric entropy.
. There are two notions of covering number, internal and external, along with the packing number and the metric entropy.
- The packing number
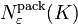 is the largest number of points
is the largest number of points 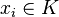 such that the balls
such that the balls 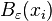 fit within K and are pairwise disjoint.
fit within K and are pairwise disjoint. - The internal covering number
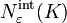 is the fewest number of points
is the fewest number of points 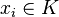 such that the balls
such that the balls 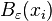 cover
cover  .
. - The external covering number
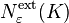 is the fewest number of points
is the fewest number of points 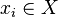 such that the balls
such that the balls 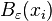 cover
cover  .
. - The metric entropy
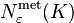 is the largest number of points
is the largest number of points 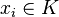 such that the points are
such that the points are  -separated, i.e.
-separated, i.e. 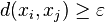 for all
for all 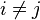 .
.
Inequalities and Monotonicity
The internal and external covering numbers, the packing number, and the metric entropy are all closely related. The following chain of inequalities holds for any 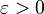 .[1]
.[1]
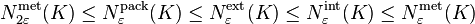
In addition, the quantities 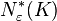 are non-increasing in
are non-increasing in  and non-decreasing in
and non-decreasing in  for each of
for each of 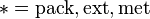 . However, monotonicity in
. However, monotonicity in  can in general fail for
can in general fail for 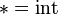 .
.
References
- ↑ Tao, Terrance. "Metric entropy analogues of sum set theory". Retrieved 2 June 2014.