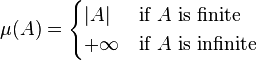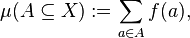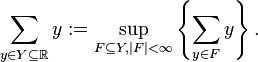Counting measure

In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset has finitely many elements, and ∞ if the subset is infinite.^[1]

The counting measure can be defined on any measurable set, but is mostly used on countable sets.^[1]

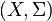In formal notation, we can make any set X into a measurable space by taking the sigma-algebra $\Sigma$ of measurable subsets to consist of all subsets of $X$ . Then the counting measure $\mu$ on this measurable space $(X,\Sigma)$ is the positive measure $\Sigma\rightarrow[0,+\infty]$ defined by

\mu(A)=\begin{cases} \vert A \vert & \text{if } A \text{ is finite}\\ +\infty & \text{if } A \text{ is infinite} \end{cases}

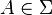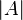for all $A\in\Sigma$ , where $\vert A\vert$ denotes the cardinality of the set $A$ .^[2]

The counting measure on 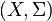$(X,\Sigma)$ is σ-finite if and only if the space $X$ is countable.^[3]

Discussion

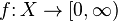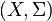The counting measure is a special case of a more general construct. With the notation as above, any function $f \colon X \to [0, \infty)$ defines a measure $\mu$ on $(X, \Sigma)$ via

\mu(A \subseteq X):=\sum_{a \in A} f(a),

where the possibly uncountable sum of real numbers is defined to be the sup of the sums over all finite subsets, i.e.,

\sum_{y \in Y \subseteq \mathbb R} y := \sup_{F \subseteq Y, |F| < \infty} \left\{ \sum_{y \in F} y \right\}.

Taking f(x)=1 for all x in X produces the counting measure.

Notes

↑ 1.0 1.1 Counting Measure at PlanetMath.org.
↑ Schilling (2005), p.27
↑ Hansen (2009) p.47

References

Schilling, René L. (2005)."Measures, Integral and Martingales". Cambridge University Press.
Hansen, Ernst (2009)."Measure theory, Fourth Edition". Department of Mathematical Science, University of Copenhagen.