Count-distinct problem
In computer science, the count-distinct problem[1] (also known in applied mathematics as the cardinality estimation problem) is the problem of finding the number of distinct elements in a data stream with repeated elements. This is a well-known problem with numerous applications. The elements might represent IP addresses of packets passing through a router, unique visitors to a web site, elements in a large database, motifs in a DNA sequence, or elements of RFID/sensor networks.
Formal definition
- Instance: A stream of elements
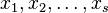 with repetitions, and an integer
with repetitions, and an integer  . Let
. Let  be the number of distinct elements, namely
be the number of distinct elements, namely 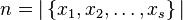 , and let these elements be
, and let these elements be 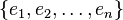 .
. - Objective: Find an estimate
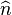 of
of  using only
using only  storage units, where
storage units, where 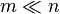 .
.
An example of an instance for the cardinality estimation problem is the stream: 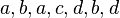 . For this instance,
. For this instance, 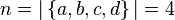 .
.
Naive solution
The naive solution to the problem is as follows:
Initialize a counter,, to zero,
. Initialize an efficient dictionary data structure,
, such as hash table or search tree in which insertion and membership can be performed quickly. For each element
, a membership query is issued. If
is not a member of
(
) Add
to
Increase
by one,
Otherwise (
) do nothing. Output
.
As long as the number of distinct elements is not too big,  fits in main memory and an exact answer can be retrieved.
However, this approach does not scale for bounded storage, or if the computation performed for each element
fits in main memory and an exact answer can be retrieved.
However, this approach does not scale for bounded storage, or if the computation performed for each element 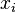 should be minimized. In such a case, several streaming algorithms have been proposed which use a fixed number of storage units.
should be minimized. In such a case, several streaming algorithms have been proposed which use a fixed number of storage units.
Streaming algorithms
To handle the bounded storage constraint, streaming algorithms use a randomization to produce a non-exact estimation of the distinct number of elements,  .
State-of-the-art estimators hash every element
.
State-of-the-art estimators hash every element 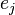 into a low dimensional data sketch using a hash function,
into a low dimensional data sketch using a hash function, 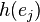 .
The different techniques can be classified according to the data sketches they store.
.
The different techniques can be classified according to the data sketches they store.
Min/max sketches
Min/max sketches [2] [3] store only the minimum/maximum hashed values. Examples of known min/max sketch estimators: Chassaing et al. [4] presents max sketch which is the minimum-variance unbiased estimator for the problem. The continuous max sketches estimator [5] is the maximum likelihood estimator. The best known estimator is the HyperLogLog algorithm [6] it offers the best tradeoff between precision and storage size.
The intuition behind such estimators is that each sketch carries information about the desired quantity. For example, when every element 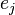 is associated with a uniform RV,
is associated with a uniform RV, 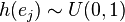 , the expected minimum value of
, the expected minimum value of 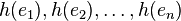 is
is 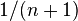 .
The hash function guarantees that
.
The hash function guarantees that 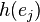 is identical for all the appearances of
is identical for all the appearances of 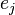 . Thus, the existence of duplicates does not affect the value of the extreme order statistics.
. Thus, the existence of duplicates does not affect the value of the extreme order statistics.
There are other estimation techniques other than min/max sketches. The first paper on count-distinct estimation by Flajolet et al. [7] describes a bit pattern sketch. In this case, the elements are hashed into a bit vector and the sketch holds the logical OR of all hashed values.
Bottom-m sketches
Bottom-m sketches
[8]
are a generalization of min sketches, which maintain the  minimal values, where
minimal values, where 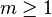 .
See Cosma et al.[2] for a theoretical overview of count-distinct estimation algorithms, and Metwally
[9]
for a practical overview with comparative simulation results.
.
See Cosma et al.[2] for a theoretical overview of count-distinct estimation algorithms, and Metwally
[9]
for a practical overview with comparative simulation results.
Weighted count-distinct problem
In its weighted version, each element is associated with a weight and the goal is to estimate the total sum of weights. Formally,
- Instance: A stream of weighted elements
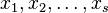 with repetitions, and an integer
with repetitions, and an integer  . Let
. Let  be the number of distinct elements, namely
be the number of distinct elements, namely 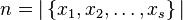 , and let these elements be
, and let these elements be 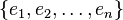 . Finally, let
. Finally, let 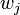 be the weight of
be the weight of 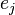 .
. - Objective: Find an estimate
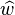 of
of 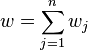 using only
using only  storage units, where
storage units, where 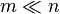 .
.
An example of an instance for the weighted problem is: 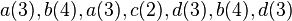 . For this instance,
. For this instance, 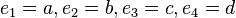 , the weights are
, the weights are 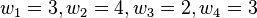 and
and 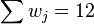 .
.
As an application example, 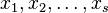 could be IP packets received by a server. Each packet belongs to one of
could be IP packets received by a server. Each packet belongs to one of  IP flows
IP flows 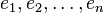 . The weight
. The weight 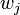 can be the load imposed by flow
can be the load imposed by flow 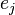 on the server. Thus,
on the server. Thus, 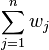 represents the total load imposed on the server by all the flows to which packets
represents the total load imposed on the server by all the flows to which packets 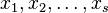 belong.
belong.
Solving the weighted count-distinct problem
Any extreme order statistics estimator (min/max sketches) for the unweighted problem can be generalized to an estimator for the weighted problem .[10] For example, the weighted estimator proposed by Cohen et al.[5] can be obtained when the continuous max sketches estimator is extended to solve the weighted problem. In particular, the HyperLogLog algorithm [6] can be extended to solve the weighted problem. The extended HyperLogLog algorithm offers the best performance, in terms of statistical accuracy and memory usage, among all the other known algorithms for the weighted problem.
See also
- HyperLogLog
- Count–min sketch
- Streaming algorithm
- Maximum likelihood
- Minimum-variance unbiased estimator
References
- ↑ Ullman, Jeff; Rajaraman, Anand; Leskovec, Jure. "Mining data streams".
- ↑ 2.0 2.1 Cosma, Ioana A.; Clifford, Peter (2011). "A statistical analysis of probabilistic counting algorithms". Scandinavian Journal of Statistics.
- ↑ Giroire, Frederic; Fusy, Eric (2007). "Estimating the Number of Active Flows in a Data Stream over a Sliding Window". ANALCO.
- ↑ Chassaing, Philippe; Gerin, Lucas (2006). "Efficient estimation of the cardinality of large data sets". Proceedings of the 4th Colloquium on Mathematics and Computer Science.
- ↑ 5.0 5.1 Cohen, Edith (1997). "Size-estimation framework with applications to transitive closure and reachability". J. Comput. Syst. Sci.
- ↑ 6.0 6.1 Flajolet, Philippe; Fusy, Eric; Gandouet, Olivier; Meunier, Frederic (2007). "HyperLoglog: the analysis of a near-optimal cardinality estimation algorithm". Analysis of Algorithms (AofA) 2007.
- ↑ Flajolet, Philippe; Martin, G. Nigel (1985). "Probabilistic counting algorithms for data base applications". J. Comput. Syst. Sci. (Academic Press, Inc.).
- ↑ Cohen, Edith; Kaplan, Haim (2008). "Tighter estimation using bottom k sketches". PVLDB (Academic Press, Inc.).
- ↑ Metwally, Ahmed; Agrawal, Divyakant; Abbadi, Amr El (2008), Why go logarithmic if we can go linear?: Towards effective distinct counting of search traffic, Proceedings of the 11th international conference on Extending Database Technology: Advances in Database Technology
- ↑ Cohen, Reuven; Katzir, Liran; Yehezkel, Aviv (2014). "A Unified Scheme for Generalizing Cardinality Estimators to Sum Aggregation". Information Processing Letters.