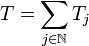Cotlar–Stein lemma
In mathematics, in the field of functional analysis, the Cotlar–Stein almost orthogonality lemma is named after mathematicians Mischa Cotlar
and Elias Stein. It may be used to obtain information on the operator norm on an operator, acting from one Hilbert space into another
when the operator can be decomposed into almost orthogonal pieces.
The original version of this lemma
(for self-adjoint and mutually commuting operators)
was proved by Mischa Cotlar in 1955[1] and allowed him to conclude that the Hilbert transform
is a continuous linear operator in 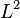 without using the Fourier transform.
A more general version was proved by Elias Stein.[2]
without using the Fourier transform.
A more general version was proved by Elias Stein.[2]
Cotlar–Stein almost orthogonality lemma
Let 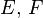 be two Hilbert spaces.
Consider a family of operators
be two Hilbert spaces.
Consider a family of operators
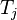 ,
, 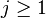 ,
with each
,
with each 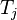 a bounded linear operator from
a bounded linear operator from  to
to 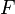 .
.
Denote
The family of operators
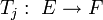 ,
, 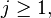 is almost orthogonal if
is almost orthogonal if
The Cotlar–Stein lemma states that if 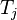 are almost orthogonal,
then the series
are almost orthogonal,
then the series
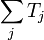 converges in the strong operator topology,
and that
converges in the strong operator topology,
and that
Proof
If R1, ..., Rn is a finite collection of bounded operators, then[3]
So under the hypotheses of the lemma,
It follows that
and that
Hence the partial sums
form a Cauchy sequence.
The sum is therefore absolutely convergent with limit satisfying the stated inequality.
To prove the inequality above set
with |aij| ≤ 1 chosen so that
Then
Hence
Taking 2mth roots and letting m tend to ∞,
which immediately implies the inequality.
Generalization
There is a generalization of the Cotlar–Stein lemma with sums replaced by integrals.[4] Let X be a locally compact space and μ a Borel measure on X. Let T(x) be a map from X into bounded operators from E to F which is uniformly bounded and continuous in the strong operator topology. If
are finite, then the function T(x)v is integrable for each v in E with
The result can be proved by replacing sums by integrals in the previous proof or by using Riemann sums to approximate the integrals.
Example
Here is an example of an orthogonal family of operators. Consider the inifite-dimensional matrices
and also
Then
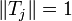 for each
for each 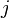 ,
hence the series
,
hence the series 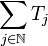 does not converge in the uniform operator topology.
does not converge in the uniform operator topology.
Yet, since
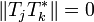 and
and
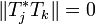 for
for 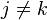 ,
the Cotlar–Stein almost orthogonality lemma tells us that
,
the Cotlar–Stein almost orthogonality lemma tells us that
converges in the strong operator topology and is bounded by 1.
Notes
References
- Cotlar, Mischa (1955), "A combinatorial inequality and its application to L2 spaces", Math. Cuyana 1: 41–55
- Hörmander, Lars (1994), Analysis of Partial Differential Operators III: Pseudodifferential Operators (2nd ed.), Springer-Verlag, pp. 165–166, ISBN 978-3-540-49937-4
- Knapp, Anthony W.; Stein, Elias (1971), "Intertwining operators for semisimple Lie groups", Ann. Math. 93: 489–579
- Stein, Elias (1993), Harmonic Analysis: Real-variable Methods, Orthogonality and Oscillatory Integrals, Princeton University Press, ISBN 0-691-03216-5


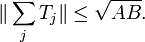
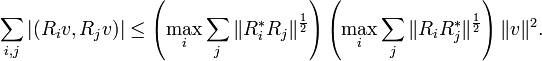
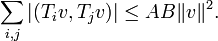
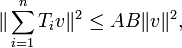
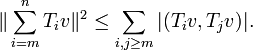
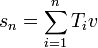
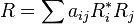
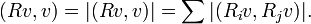
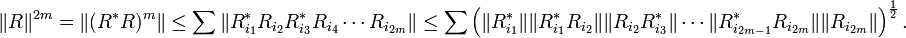
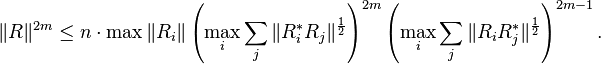
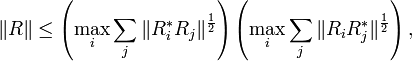
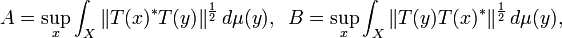
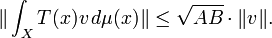
![T=\left[
\begin{array}{cccc}
1&0&0&\vdots\\0&1&0&\vdots\\0&0&1&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right]](../I/m/dd5e0118217249d3a0f5b7355eef0b0d.png)
![\qquad
T_1=\left[
\begin{array}{cccc}
1&0&0&\vdots\\0&0&0&\vdots\\0&0&0&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right],
\qquad
T_2=\left[
\begin{array}{cccc}
0&0&0&\vdots\\0&1&0&\vdots\\0&0&0&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right],
\qquad
T_3=\left[
\begin{array}{cccc}
0&0&0&\vdots\\0&0&0&\vdots\\0&0&1&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right],
\qquad
\dots.](../I/m/abff3b6cac0a98f0f763d50d8d0ae0a8.png)