Cosheaf
In topology, a branch of mathematics, a cosheaf with values in an ∞-category C that admits colimit is a functor F from the category of open subsets of a topological space X (more precisely its nerve) to C such that
- (1) The F of the empty set is the initial object.
- (2) For any increasing sequence
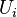 of open subsets with union U, the canonical map
of open subsets with union U, the canonical map 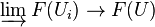 is an equivalence.
is an equivalence. - (3)
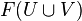 is the pushout of
is the pushout of 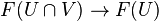 and
and 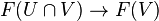 .
.
The basic example is 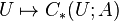 where on the right is the singular chain complex of U with coefficients in an abelian group A.
where on the right is the singular chain complex of U with coefficients in an abelian group A.
Example:[1] If f is a continuous map, then 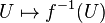 is a cosheaf.
is a cosheaf.
See also
Notes
References
- http://www.math.harvard.edu/~lurie/282ynotes/LectureVIII-Poincare.pdf
- http://arxiv.org/pdf/1303.3255v1.pdf , section 3, in particular Thm 3.10 p.34