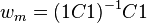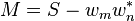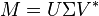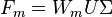Correspondence analysis

Correspondence analysis (CA) is a multivariate statistical technique proposed[1] by Hirschfeld[2] and later developed by Jean-Paul Benzécri.[3] It is conceptually similar to principal component analysis, but applies to categorical rather than continuous data. In a similar manner to principal component analysis, it provides a means of displaying or summarising a set of data in two-dimensional graphical form.

All data should be nonnegative and on the same scale for CA to be applicable, and the method treats rows and columns equivalently. It is traditionally applied to contingency tables — CA decomposes the chi-squared statistic associated with this table into orthogonal factors. Because CA is a descriptive technique, it can be applied to tables whether or not the 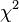χ² statistic is appropriate.[4][5]

Details

Like principal components analysis, correspondence analysis creates orthogonal components and, for each item in a table, a set of scores (sometimes called factor scores, see Factor analysis). Correspondence analysis is performed on a contingency table, C, of size m×n where m is the number of rows and n is the number of columns.

Preprocessing

From table C, compute a set of weights for the columns and the rows (sometimes called masses),[6][7] where row weights are

w_m = (1C1)^{-1} C1

and column weights are

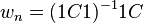w_n = (1C1)^{-1} 1C.

Next, compute a table S (called the stochastic matrix), where C is divided by the sum of C

S = (1C1)^{-1} C.

Finally, compute a table M from S and the weights as such

M = S-w_{m}w_{n}^{*}

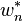where w_{n}^{*} denotes the conjugate transpose of w_{n}.

Orthogonal components

The table M is then decomposed with the generalized singular value decomposition where the left and right singular vectors are constrained by weights. The weights are diagonal tables

W_{m} = diag\{w_{m}\}

and

W_{n} = diag\{w_{n}\}

where the diagonal elements of 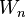W_{n} are w_{n} and the off-diagonal elements are all 0.

M is then decomposed via the generalized singular value decomposition

M = U\Sigma V^* \,

where

U^* W_m U = V^* W_n V = I..

Factor scores

Factor scores for the row items of table C are

F_{m} = W_{m} U \Sigma

and for the column items

F_{n} = W_{n} V \Sigma.

Extensions and applications

Several variants of CA are available, including detrended correspondence analysis (DCA) and canonical correspondence analysis (CCA). The extension of correspondence analysis to many categorical variables is called multiple correspondence analysis. An adaptation of correspondence analysis to the problem of discrimination based upon qualitative variables (i.e., the equivalent of discriminant analysis for qualitative data) is called discriminant correspondence analysis or barycentric discriminant analysis.

In the social sciences, correspondence analysis, and particularly its extension multiple correspondence analysis, was made known outside France through French sociologist Pierre Bourdieu's application of it.[8]

Implementations

See also

References

  1. ↑ Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP ISBN 0-19-850994-4
  2. ↑ Hirschfeld, H.O. (1935) "A connection between correlation and contingency", Proc. Cambridge Philosophical Society, 31, 520–524
  3. ↑ Benzécri, J.-P. (1973). L'Analyse des Données. Volume II. L'Analyse des Correspondances. Paris, France: Dunod.
  4. ↑ Greenacre, Michael (1983). Theory and Applications of Correspondence Analysis. London: Academic Press. ISBN 0-12-299050-1.
  5. ↑ Greenacre, Michael (2007). Correspondence Analysis in Practice, Second Edition. London: Chapman & Hall/CRC.
  6. ↑ Greenacre, Michael (1983). Theory and Applications of Correspondence Analysis. London: Academic Press. ISBN 0-12-299050-1.
  7. ↑ Greenacre, Michael (2007). Correspondence Analysis in Practice, Second Edition. London: Chapman & Hall/CRC.
  8. ↑ Bourdieu, Pierre (1984). Distinction. Routledge. p. 41. ISBN 0674212770.
  9. ↑ Nenadic, O. and Greenacre, M. (2007) "Correspondence analysis in R, with two- and three-dimensional graphics: the ca package", Journal of Statistical Software, 20(3)

External links