Cornacchia's algorithm

In computational number theory, Cornacchia's algorithm is an algorithm for solving the Diophantine equation 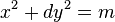x^2+dy^2=m, where 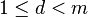1\le d<m and d and m are coprime. The algorithm was described in 1908 by Giuseppe Cornacchia.[1]

The algorithm

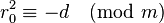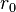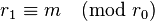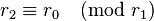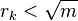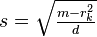First, find any solution to r_0^2\equiv-d\pmod m; if no such r_0 exist, there can be no primitive solution to the original equation. Then use the Euclidean algorithm to find r_1\equiv m\pmod{r_0}, r_2\equiv r_0\pmod{r_1} and so on; stop when r_k<\sqrt m. If s=\sqrt{\tfrac{m-r_k^2}d} is an integer, then the solution is 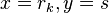x=r_k,y=s; otherwise there is no solution.

Example

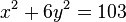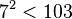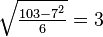Solve the equation x^2+6y^2=103. A square root of −6 (mod 103) is 32, and 103 ≡ 7 (mod 32); since 7^2<103 and \sqrt{\tfrac{103-7^2}6}=3, there is a solution x = 7, y = 3.

References

  1. ↑ Cornacchia, G. (1908). "Su di un metodo per la risoluzione in numeri interi dell' equazione 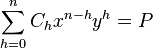\sum_{h=0}^nC_hx^{n-h}y^h=P.". Giornale di Matematiche di Battaglini 46: 33–90.

External links

Basilla, Julius Magalona (12 May 2004). 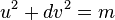u^2+dv^2=m (PDF).