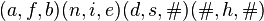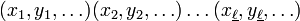Convolution (computer science)
In computer science, specifically formal languages, convolution (sometimes referred to as zip) is a function which maps a tuple of sequences into a sequence of tuples.
Example
Given the three words and, fish and be where |and| is 3, |fish| is 4 and |be| is 2. Let 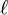 denote the longest word which is fish;
denote the longest word which is fish; 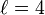 . The convolution of and, fish, be is then 4 tuples of elements:
. The convolution of and, fish, be is then 4 tuples of elements:
where # is a symbol not in the original alphabet. In Haskell this truncates to shortest sequence 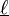 , where
, where 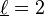 :
:
zip3 "and" "fish" "be" -- [('a','f','b'),('n','i','e')]
Definition
Let Σ be an alphabet, # a symbol not in Σ.
Let x1x2... x|x|, y1y2... y|y|, z1z2... z|z|, ... be n words (i.e. finite sequences) of elements of Σ. Let 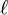 denote the length of the longest word, i.e. the maximum of |x|, |y|, |z|, ... .
denote the length of the longest word, i.e. the maximum of |x|, |y|, |z|, ... .
The convolution of these words is a finite sequence of n-tuples of elements of (Σ ∪ {#}), i.e. an element of 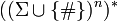 :
:
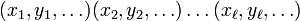 ,
,
where for any index i > |w|, the wi is #.
The convolution of x, y, z, ... is denoted conv( x, y, z, ...), zip( x, y, z, ...) or x ⋆ y ⋆ z ⋆ ...
The inverse to convolution is sometimes denoted unzip.
A variation of the convolution operation is defined by:
where 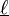 is the minimum length of the input words. It avoids the use of an adjoined element
is the minimum length of the input words. It avoids the use of an adjoined element 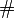 , but destroys information about elements of the input sequences beyond
, but destroys information about elements of the input sequences beyond 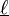 .
.
In programming languages
Convolution functions are often available in programming languages, often referred to as zip. In Lisp-dialects one can simply map the desired function over the desired lists, map is variadic in Lisp so it can take an arbitrary amount of lists as argument. An example from Clojure:[1]
;; `nums' contains an infinite list of numbers (0 1 2 3 ...) (def nums (range)) (def tens [10 20 30]) (def firstname "Alice") ;; To convolve (0 1 2 3 ...) and [10 20 30] into a vector, invoke `map vector' on them; same with list (map vector nums tens) ; ⇒ ([1 10] [2 20] [3 30]) (map list nums tens) ; ⇒ ((1 10) (2 20) (3 30)) (map str nums tens) ; ⇒ ("110" "220" "330") ;; `map' truncates to the shortest sequence; note missing \c and \e from "Alice" (map vector nums tens firstname) ; ⇒ ([1 10 \A] [2 20 \l] [3 30 \i]) (map str nums tens firstname) ; ⇒ ("110A" "220l" "330i") ;; To unzip, apply `map vector' or `map list' (apply map list (map vector nums tens firstname)) ;; ⇒ ((0 1 2) (10 20 30) (\A \l \i))
In Common Lisp:
(defparameter nums '(1 2 3)) (defparameter tens '(10 20 30)) (defparameter firstname "Alice") (mapcar #'list nums tens) ;; ⇒ ((1 10) (2 20) (3 30)) (mapcar #'list nums tens (coerce firstname 'list)) ;; ⇒ ((1 10 #\A) (2 20 #\l) (3 30 #\i)) — truncates on shortest list ;; Unzips (apply #'mapcar #'list (mapcar #'list nums tens (coerce firstname 'list))) ;; ⇒ ((1 2 3) (10 20 30) (#\A #\l #\i))
Languages such as Python provide a zip() function, older version (Python 2.*) allowed mapping None over lists to get a similar effect.[2] zip() in conjunction with the * operator unzips a list:[2]
nums = [1, 2, 3] tens = [10, 20, 30] firstname = 'Alice' zipped = zip(nums, tens) zipped # ⇒ [(1, 10), (2, 20), (3, 30)] — zip zip(*zipped) # ⇒ [(1, 2, 3), (10, 20, 30)] — unzip zipped2 = zip(nums, tens, list(firstname)) zipped2 # ⇒ [(1, 10, 'A'), (2, 20, 'l'), (3, 30, 'i')] — zip, truncates on shortest zip(*zipped2) # ⇒ [(1, 2, 3), (10, 20, 30), ('A', 'l', 'i')] — unzip # mapping with `None' doesn't truncate; deprecated in Python 3.* map(None,nums, tens, list(firstname)) # ⇒ [(1, 10, 'A'), (2, 20, 'l'), (3, 30, 'i'), (None, None, 'c'), (None, None, 'e')]
Haskell has a method of convolving sequences but requires a specific function for each arity (zip for two sequences, zip3 for three etc.),[3] similarly the functions unzip and unzip3 are available for unzipping:
-- nums contains an infinite list of numbers [1, 2, 3,...] nums = [1..] tens = [10, 20, 30] firstname = "Alice" zip nums tens -- ⇒ [(1,10),(2,20),(3,30)] — zip, truncates infinite list unzip $ zip nums tens -- ⇒ ([1,2,3],[10,20,30]) — unzip zip3 nums tens firstname -- ⇒ [(1,10,'A'),(2,20,'l'),(3,30,'i')] — zip, truncates unzip3 $ zip3 nums tens firstname -- ⇒ ([1,2,3],[10,20,30],"Ali") — unzip
Language comparison
List of languages by support of convolution:
| Language | Zip | Zip 3 lists | Zip n lists | Notes |
|---|---|---|---|---|
| Clojure | (map list list1 list2) (map vector list1 list2) |
(map vector list1 list2 list3) (map vector list1 list2 list3) |
(map list list1 … listn) (map vector list1 … listn) |
Stops after the length of the shortest list. |
| Common Lisp | (mapcar #'list list1 list2) | (mapcar #'list list1 list2 list3) | (mapcar #'list list1 ... listn) | Stops after the length of the shortest list. |
| Haskell | zip list1 list2 | zip3 list1 list2 list3 | zipn list1 … listn | zipn for n > 3 is available in the module Data.List. Stops after the shortest list ends. |
| Python | zip(list1, list2) | zip(list1, list2, list3) | zip(list1, …, listn) | zip() and map() (3.x) stops after the shortest list ends, whereas map() (2.x) and itertools.zip_longest() (3.x) extends the shorter lists with None items |
| Ruby | list1.zip(list2) | list1.zip(list2, list3) | list1.zip(list1, .., listn) | When the list being executed upon (list1) is shorter than the lists being zipped the resulting list is the length of list1. If list1 is longer nil values are used to fill the missing values[4] |
| Language | Unzip | Unzip 3 tuples | Unzip n tuples | Notes |
|---|---|---|---|---|
| Clojure | (apply map vector convlist) | (apply map vector convlist) | (apply map vector convlist) | |
| Common Lisp | (apply #'mapcar #'list convlist) | (apply #'mapcar #'list convlist) | (apply #'mapcar #'list convlist) | |
| Haskell | unzip convlist | unzip3 convlist | unzipn convlist | unzipn for n > 3 is available in the module Data.List. |
| Python | zip(*convvlist) | zip(*convvlist) | zip(*convvlist) |
See also
References
- ↑ map from ClojureDocs
- ↑ 2.0 2.1 map(function, iterable, ...) from section Built-in Functions from Python v2.7.2 documentation
- ↑ zip :: [a] -> [b] -> [(a, b)] from Prelude, Basic libraries
- ↑ http://www.ruby-doc.org/core-2.0/Array.html#method-i-zip
This article incorporates material from convolution on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.