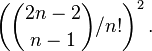Convex position
In discrete and computational geometry, a set of points in the Euclidean plane is said to be in convex position or convex independent if none of the points can be represented as a convex combination of the others.[1] A finite set of points is in convex position if all of the points are vertices of their convex hull.[1] More generally, a family of convex sets is said to be in convex position if they are pairwise disjoint and none of them is contained in the convex hull of the others.[2]
An assumption of convex position can make certain computational problems easier to solve. For instance, the traveling salesman problem, NP-hard for arbitrary sets of points in the plane, is trivial for points in convex position: the optimal tour is the convex hull.[3] Similarly, the minimum-weight triangulation is NP-hard for arbitrary point sets,[4] but solvable in polynomial time by dynamic programming for points in convex position.[5]
The Erdős–Szekeres theorem guarantees that every set of n points in general position (no three in a line) has at least a logarithmic number of points in convex position.[6] If n points are chosen uniformly at random in a unit square, the probability that they are in convex position is[7]
References
- ↑ 1.0 1.1 Matoušek, Jiří (2002), Lectures on Discrete Geometry, Graduate Texts in Mathematics, Springer-Verlag, p. 30, ISBN 978-0-387-95373-1.
- ↑ Tóth, Géza; Valtr, Pavel (2005), "The Erdős-Szekeres theorem: upper bounds and related results", Combinatorial and computational geometry, Math. Sci. Res. Inst. Publ. 52, Cambridge: Cambridge Univ. Press, pp. 557–568, MR 2178339.
- ↑ Deĭneko, Vladimir G.; Hoffmann, Michael; Okamoto, Yoshio; Woeginger, Gerhard J. (2006), "The traveling salesman problem with few inner points", Operations Research Letters 34 (1): 106–110, doi:10.1016/j.orl.2005.01.002, MR 2186082.
- ↑ Mulzer, Wolfgang; Rote, Günter (2008), "Minimum-weight triangulation is NP-hard", Journal of the ACM 55 (2), Article A11, arXiv:cs.CG/0601002, doi:10.1145/1346330.1346336.
- ↑ Klincsek, G. T. (1980), "Minimal triangulations of polygonal domains", Annals of Discrete Mathematics 9: 121–123, doi:10.1016/s0167-5060(08)70044-x.
- ↑ Erdős, Paul; Szekeres, George (1935), "A combinatorial problem in geometry", Compositio Mathematica 2: 463–470.
- ↑ Valtr, P. (1995), "Probability that n random points are in convex position", Discrete and Computational Geometry 13 (3-4): 637–643, doi:10.1007/BF02574070, MR 1318803.