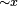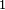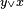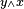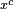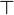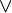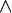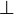Converse nonimplication
In logic, converse nonimplication[1] is a logical connective which is the negation of the converse of implication.
Definition
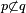 which is the same as
which is the same as 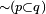
Truth table
The truth table of 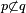 .[2]
.[2]
| p | q | 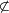 |
|---|---|---|
| T | T | F |
| T | F | F |
| F | T | T |
| F | F | F |
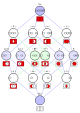
Venn diagram
The Venn Diagram of "It is not the case that B implies A" (the red area is true)

Properties
falsehood-preserving: The interpretation under which all variables are assigned a truth value of 'false' produces a truth value of 'false' as a result of converse nonimplication
Symbol
Alternatives for 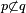 are
are
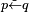 :
: 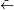 combines Converse implication's left arrow(
combines Converse implication's left arrow(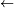 ) with Negation's tilde(
) with Negation's tilde(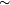 ).
).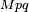 : uses prefixed capital letter.
: uses prefixed capital letter. 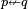 :
:  combines Converse implication's left arrow(
combines Converse implication's left arrow(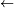 ) denied by means of a stroke(
) denied by means of a stroke(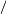 ).
).
Natural language
Rhetorical
"not A but B"
Boolean algebra
Converse Nonimplication in a general Boolean algebra is defined as 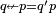 .
.
Example of a 2-element Boolean algebra: the 2 elements {0,1} with 0 as zero and 1 as unity element, operators 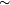 as complement operator,
as complement operator,  as join operator and
as join operator and  as meet operator, build the Boolean algebra of propositional logic.
as meet operator, build the Boolean algebra of propositional logic.
|
and |
|
and |
|
then 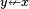 means means |
| ||||||||||||||||||||||||||||||||||||||||||
| (Negation) | (Inclusive Or) | (And) | (Converse Nonimplication) |
[4]
Example of a 4-element Boolean algebra: the 4 divisors {1,2,3,6} of 6 with 1 as zero and 6 as unity element, operators  (codivisor of 6) as complement operator,
(codivisor of 6) as complement operator,  (least common multiple) as join operator and
(least common multiple) as join operator and  (greatest common divisor) as meet operator, build a Boolean algebra.
(greatest common divisor) as meet operator, build a Boolean algebra.
|
and |
|
and |
|
then 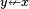 means means |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (Codivisor 6) | (Least Common Multiple) | (Greatest Common Divisor) | (x's greatest Divisor coprime with y) |
Properties
Non-associative
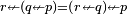 iff
iff 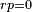 [5] (In a two-element Boolean algebra the latter condition is reduced to
[5] (In a two-element Boolean algebra the latter condition is reduced to 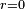 or
or 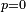 ). Hence in a nontrivial Boolean algebra Converse Nonimplication is nonassociative.
). Hence in a nontrivial Boolean algebra Converse Nonimplication is nonassociative.
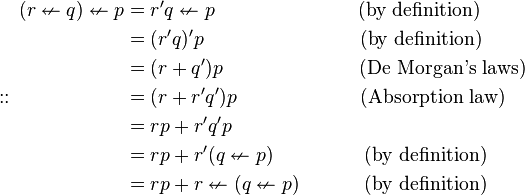
Clearly, it is associative iff 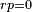 .
.
Non-commutative
-
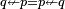 iff
iff 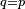 [6]. Hence Converse Nonimplication is noncommutative.
[6]. Hence Converse Nonimplication is noncommutative.
Neutral and absorbing elements
-
 is a left neutral element (
is a left neutral element (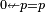 ) and a right absorbing element (
) and a right absorbing element (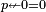 ).
). -
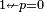 ,
, 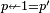 , and
, and 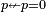 .
. - Implication
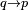 is the dual of Converse Nonimplication
is the dual of Converse Nonimplication 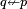 [7].
[7].
[6]
| Converse Nonimplication is noncommutative | ||||
|---|---|---|---|---|
| Step | Make use of | Resulting in | ||
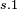 |
Definition | 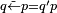 | ||
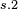 |
Definition | 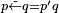 | ||
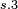 |
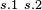 |
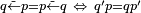 | ||
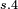 |
 |
 |
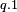 | |
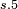 |
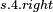 - expand Unit element - expand Unit element |
 |
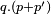 | |
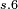 |
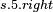 - evaluate expression - evaluate expression |
 |
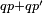 | |
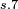 |
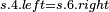 |
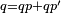 | ||
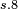 |
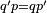 |
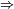 |
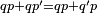 | |
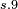 |
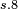 - regroup common factors - regroup common factors |
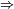 |
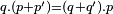 | |
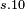 |
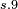 - join of complements equals unity - join of complements equals unity |
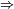 |
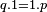 | |
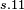 |
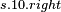 - evaluate expression - evaluate expression |
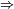 |
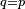 | |
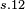 |
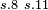 |
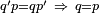 | ||
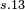 |
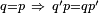 | |||
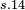 |
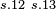 |
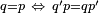 | ||
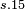 |
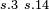 |
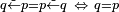 | ||
[7]
| Implication is the dual of Converse Nonimplication | ||||
|---|---|---|---|---|
| Step | Make use of | Resulting in | ||
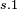 |
Definition | 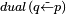 |
 |
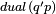 |
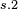 |
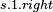 - .'s dual is + - .'s dual is + |
 |
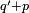 | |
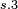 |
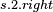 - Involution complement - Involution complement |
 |
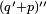 | |
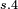 |
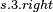 - De Morgan's laws applied once - De Morgan's laws applied once |
 |
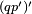 | |
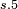 |
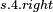 - Commutative law - Commutative law |
 |
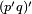 | |
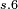 |
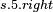 |
 |
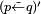 | |
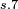 |
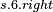 |
 |
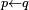 | |
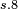 |
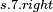 |
 |
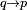 | |
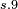 |
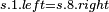 |
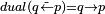 | ||
Computer science
An example for converse nonimplication in computer science can be found when performing a right outer join on a set of tables from a database, if records not matching the join-condition from the "left" table are being excluded.[3]
Notes
- ↑ Lehtonen, Eero, and Poikonen, J.H.
- ↑ Knuth 2011, p. 49
- ↑ http://www.codinghorror.com/blog/2007/10/a-visual-explanation-of-sql-joins.html
References
- Knuth, Donald E. (2011). The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1 (1st ed.). Addison-Wesley Professional. ISBN 0-201-03804-8.
| ||||||||||||||||||||||||