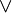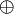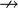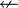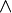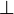Converse implication
Converse implication is the converse of implication. That is to say; that for any two propositions P and Q, if Q implies P, then P is the converse implication of Q.
It may take the following forms:
- p⊂q, Bpq, or p←q
Definition
Truth table
The truth table of A⊂B
| a | b | ⊂ |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | F |
| F | F | T |
Venn diagram
The Venn diagram of "If B then A" (the white area shows where the statement is false)
Properties
truth-preserving: The interpretation under which all variables are assigned a truth value of 'true' produces a truth value of 'true' as a result of converse implication.
Natural language
"Not q without p."
"p if q."
Boolean Algebra
(A + B')
See also
| ||||||||||||||||||||||||
