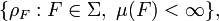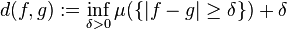Convergence in measure

Convergence in measure can refer to two distinct mathematical concepts which both generalize the concept of convergence in probability.

Definitions

Let 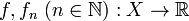$f, f_n\ (n \in \mathbb N): X \to \mathbb R$ be measurable functions on a measure space (X,Σ,μ). The sequence (f_n) is said to converge globally in measure to f if for every ε > 0,

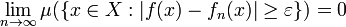\lim_{n\to\infty} \mu(\{x \in X: |f(x)-f_n(x)|\geq \varepsilon\}) = 0

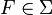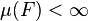and to converge locally in measure to f if for every ε > 0 and every $F \in \Sigma$ with $\mu (F) < \infty$ ,

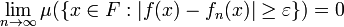\lim_{n\to\infty} \mu(\{x \in F: |f(x)-f_n(x)|\geq \varepsilon\}) = 0

Convergence in measure can refer to either global convergence in measure or local convergence in measure, depending on the author.

Properties

Throughout, f and f_n (n 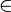$\in$ N) are measurable functions X → R.

Global convergence in measure implies local convergence in measure. The converse, however, is false; i.e., local convergence in measure is strictly weaker than global convergence in measure, in general.

If, however, 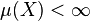$\mu (X)<\infty$ or, more generally, if all the f_n vanish outside some set of finite measure, then the distinction between local and global convergence in measure disappears.

If μ is σ-finite and (f_n) converges (locally or globally) to f in measure, there is a subsequence converging to f almost everywhere. The assumption of σ-finiteness is not necessary in the case of global convergence in measure.

If μ is σ-finite, (f_n) converges to f locally in measure if and only if every subsequence has in turn a subsequence that converges to f almost everywhere.

In particular, if (f_n) converges to f almost everywhere, then (f_n) converges to f locally in measure. The converse is false.

Fatou's lemma and the monotone convergence theorem hold if almost everywhere convergence is replaced by (local or global) convergence in measure.

If μ is σ-finite, Lebesgue's dominated convergence theorem also holds if almost everywhere convergence is replaced by (local or global) convergence in measure.

If X = [a,b] ⊆ R and μ is Lebesgue measure, there are sequences (g_n) of step functions and (h_n) of continuous functions converging globally in measure to f.

If f and f_n (n ∈ N) are in L^p(μ) for some p > 0 and (f_n) converges to f in the p-norm, then (f_n) converges to f globally in measure. The converse is false.

If f_n converges to f in measure and g_n converges to g in measure then f_n + g_n converges to f + g in measure. Additionally, if the measure space is finite, f_ng_n also converges to fg.

Counterexamples

Let 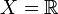$X = \mathbb R$ , μ be Lebesgue measure, and f the constant function with value zero.

The sequence 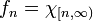$f_n = \chi_{[n,\infty)}$ converges to f locally in measure, but does not converge to f globally in measure.

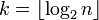The sequence $f_n = \chi_{[\frac{j}{2^k},\frac{j+1}{2^k}]}$ where $k = \lfloor \log_2 n\rfloor$ and $j=n-2^k$

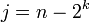
(The first five terms of which are $\chi_{\left[0,1\right]},\;\chi_{\left[0,\frac12\right]},\;\chi_{\left[\frac12,1\right]},\;\chi_{\left[0,\frac14\right]},\;\chi_{\left[\frac14,\frac12\right]}$ ) converges to 0 locally in measure; but for no x does f_n(x) converge to zero. Hence (f_n) fails to converge to f almost everywhere.

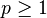The sequence $f_n = n\chi_{\left[0,\frac1n\right]}$ converges to f almost everywhere (hence also locally in measure), but not in the p-norm for any $p \geq 1$ .

Topology

There is a topology, called the topology of (local) convergence in measure, on the collection of measurable functions from X such that local convergence in measure corresponds to convergence on that topology. This topology is defined by the family of pseudometrics

\{\rho_F : F \in \Sigma,\ \mu (F) < \infty\},

where

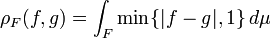\rho_F(f,g) = \int_F \min\{|f-g|,1\}\, d\mu

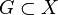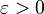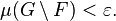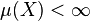In general, one may restrict oneself to some subfamily of sets F (instead of all possible subsets of finite measure). It suffices that for each $G\subset X$ of finite measure and $\varepsilon > 0$ there exists F in the family such that $\mu(G\setminus F)<\varepsilon.$ When $\mu(X) < \infty$ , we may consider only one metric 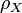$\rho_X$ , so the topology of convergence in finite measure is metrizable. If 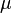$\mu$ is an arbitrary measure finite or not, then

d(f,g) := \inf\limits_{\delta>0} \mu(\{|f-g|\geq\delta\}) + \delta

still defines a metric that generates the global convergence in measure.^[1]

Because this topology is generated by a family of pseudometrics, it is uniformizable. Working with uniform structures instead of topologies allows us to formulate uniform properties such as Cauchyness.

References

↑ Vladimir I. Bogachev, Measure Theory Vol. I, Springer Science & Business Media, 2007

D.H. Fremlin, 2000. Measure Theory. Torres Fremlin.
H.L. Royden, 1988. Real Analysis. Prentice Hall.
G.B. Folland 1999, Section 2.4. Real Analysis. John Wiley & Sons.