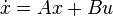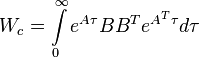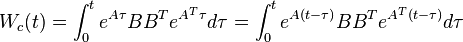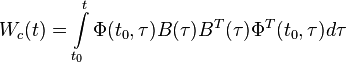Controllability Gramian
In control theory, the controllability Gramian is a Gramian used to determine whether or not a linear system is controllable. For the time-invariant linear system
if all eigenvalues of  have negative real part, then the unique solution
have negative real part, then the unique solution 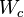 of the Lyapunov equation
of the Lyapunov equation
is positive definite if and only if the pair 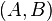 is controllable.
is controllable. 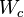 is known as the controllability Gramian and can also be expressed as
is known as the controllability Gramian and can also be expressed as
A related matrix used for determining controllability is
The pair 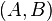 is controllable if and only if the matrix
is controllable if and only if the matrix 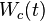 is nonsingular, for any
is nonsingular, for any 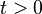 .[1][2] A physical interpretation of the controllability Gramian is that if the input to the system is white gaussian noise, then
.[1][2] A physical interpretation of the controllability Gramian is that if the input to the system is white gaussian noise, then 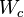 is the covariance of the state.[3]
is the covariance of the state.[3]
Linear time-variant state space models of form
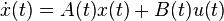 ,
,
are controllable in an interval ![[t_0,t_1]](../I/m/0b3b8cb99d808fe833d8f1c61cac6b2e.png) if and only if the rows of the matrix product
if and only if the rows of the matrix product 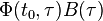 where
where 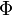 is the state transition matrix are linearly independent.
The Gramian is used to prove the linear independence of
is the state transition matrix are linearly independent.
The Gramian is used to prove the linear independence of 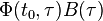 .
To have linear independence Gramian matrix
.
To have linear independence Gramian matrix 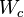 have to be nonsingular, i.e., invertible.
have to be nonsingular, i.e., invertible.
See also
References
- ↑ Controllability Gramian Lecture notes to ECE 521 Modern Systems Theory by Professor A. Manitius, ECE Department, George Mason University.
- ↑ Chen, Chi-Tsong (1999). Linear System Theory and Design Third Edition. New York, New York: Oxford University Press. p. 145. ISBN 0-19-511777-8.
- ↑ Franklin, Gene F. (2002). Feedback Control of Dynamic Systems Fourth Edition. Upper Saddle River, New Jersey: Prentice Hall. p. 854. ISBN 0-13-032393-4.