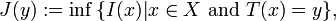Contraction principle (large deviations theory)
In mathematics — specifically, in large deviations theory — the contraction principle is a theorem that states how a large deviation principle on one space "pushes forward" to a large deviation principle on another space via a continuous function.
Statement of the theorem
Let X and Y be Hausdorff topological spaces and let (με)ε>0 be a family of probability measures on X that satisfies the large deviation principle with rate function I : X → [0, +∞]. Let T : X → Y be a continuous function, and let νε = T∗(με) be the push-forward measure of με by T, i.e., for each measurable set/event E ⊆ Y, νε(E) = με(T−1(E)). Let
with the convention that the infimum of I over the empty set ∅ is +∞. Then:
- J : Y → [0, +∞] is a rate function on Y,
- J is a good rate function on Y if I is a good rate function on X, and
- (νε)ε>0 satisfies the large deviation principle on Y with rate function J.
References
- Dembo, Amir; Zeitouni, Ofer (1998). Large deviations techniques and applications. Applications of Mathematics (New York) 38 (Second edition ed.). New York: Springer-Verlag. pp. xvi+396. ISBN 0-387-98406-2. MR 1619036. (See chapter 4.2.1)
- den Hollander, Frank (2000). Large deviations. Fields Institute Monographs 14. Providence, RI: American Mathematical Society. pp. x+143. ISBN 0-8218-1989-5. MR 1739680.