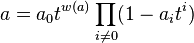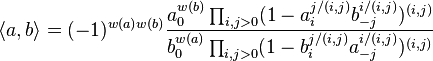Contou-Carrère symbol

In mathematics, the Contou-Carrère symbol 〈a,b〉 is a Steinberg symbol defined on pairs of invertible elements of the ring of Laurent power series over an Artinian ring k, taking values in the group of units of k. It was introduced by Contou-Carrère (1994).

Definition

If k is an Artinian local ring, then any invertible formal Laurent series a with coefficients in k can be written uniquely as

a=a_0t^{w(a)}\prod_{i\ne 0}(1-a_it^i)

where w(a) is an integer, the elements a_i are in k, and are in m if i is negative, and is a unit if i = 0.

The Contou-Carrère symbol 〈a,b〉 of a and b is defined to be

\langle a,b\rangle=(-1)^{w(a)w(b)}\frac{a_0^{w(b)}\prod_{i,j>0}(1-a_i^{j/(i,j)}b_{-j}^{i/(i,j)})^{(i,j)}} {b_0^{w(a)}\prod_{i,j>0}(1-b_i^{j/(i,j)}a_{-j}^{i/(i,j)})^{(i,j)}}

Contou-Carrère, Carlos (1994), "Jacobienne locale, groupe de bivecteurs de Witt universel, et symbole modéré", C. R. Acad. Sci. Paris Sér. I Math. (in French) 318 (8): 743–746, MR 1272340