Continuous group action
In topology, a continuous group action on a topological space X is a group action of a topological group G that is continuous: i.e.,
is a continuous map. Together with the group action, X is called a G-space.
If 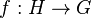 is a continuous group homomorphism of topological groups and if X is a G-space, then H can act on X by restriction:
is a continuous group homomorphism of topological groups and if X is a G-space, then H can act on X by restriction: 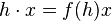 , making X a H-space. Often f is either an inclusion or a quotient map. In particular, any topological space may be thought of a G-space via
, making X a H-space. Often f is either an inclusion or a quotient map. In particular, any topological space may be thought of a G-space via 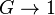 (and G would act trivially.)
(and G would act trivially.)
Two basic operations are that of taking the space of points fixed by a subgroup H and that of forming a quotient by H. We write 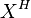 for the set of all x in X such that
for the set of all x in X such that 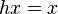 . For example, if we write
. For example, if we write 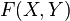 for the set of continuous maps from a G-space X to another G-space Y, then, with the action
for the set of continuous maps from a G-space X to another G-space Y, then, with the action 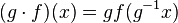 ,
,
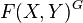 consists of f such that
consists of f such that 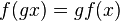 ; i.e., f is an equivariant map. We write
; i.e., f is an equivariant map. We write 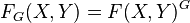 . Note, for example, for a G-space X and a closed subgroup H,
. Note, for example, for a G-space X and a closed subgroup H, 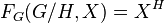 .
.
References
- John Greenlees, Peter May, Equivariant stable homotopy theory
