Continuous graph

This article is about sets of vertices and edges (graphs) defined on a continuous space. For graphs of continuous functions, see Continuous function. For connected graphs, see Connectivity (graph theory).
For graphs where each edge is a continuous line or curve, see Geometric graph theory, Topological graph theory, and Quantum graph.

In graph theory, a continuous graph is a graph whose set of vertices is a continuous space X. Continuous graphs are used as models for real-world graphs, as an alternative to other graph models such as for instance exponential random graph models.

Definition

Edges, being unordered pairs of vertices, are defined in a continuous graph by a symmetric relation[1] (i.e. subset) of the cartesian product X2 or equivalently by a symmetric function from X2 to the set {0, 1} . This could represent 1 for an edge between two vertices, and 0 for no edge, or it could represent a complete graph with a 2-color edge coloring. In this context, the set {0,1} is often denoted by 2, so we have f(X2)→2. For multi-colorings of edges we would have f(X2)→n.[2][3][4] The value of the function f(x,y) for x=y, i.e. whether the relation is reflexive determines whether the graph has loops or not but this isn't usually considered as it doesn't make much difference to the theory.[1] In descriptive set theory the spaces of interest are perfect separable Polish spaces and related spaces.[5][6]

Given a finite graph H and a continuous or discrete graph G, the homomorphism density t(H,G) is defined to be the proportion of injective maps from the vertex set of H to vertex set of G which is a graph homomorphism. For instance, if H consists of two vertices joined by a single edge, t(H,G) is the edge density of G. A sequence of finite (dense) graphs Gn is said to be convergent if, for each fixed finite graph H, the homomorphism densities t(H,Gn) are a convergent sequence of numbers. A continuous graph G is said to be a limit of such a sequence if t(H,Gn) converges to t(H,G) for each H, in which case we refer to G as a graphon. Such a limit is a symmetric measurable function in two variables,[7] that can often be written f(X2)→[0,1] which is the same as a complete continuous graph where the edges have values in the interval [0,1]. It can be shown that any sequence of dense graphs has a convergent subsequence, whose limit is a graphon which is unique up to measure rearrangement.[8] A key tool used in the proof of this claim is the Szemerédi regularity lemma.

For instance, for each natural number n, let Gn be a complete bipartite graph between two sets of n vertices. Then in the limit 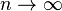n \to \infty, Gn converges to the graphon described by the function f([0,1]2)→[0,1] defined by setting f(x,y)=1 when x \in [0,1/2), y \in [1/2,1] or y \in [0,1/2), x \in [1/2,1], and f(x,y)=0 otherwise.

Graphons can be used to establish results in the property testing of graphs.[9]

For any sets X and Y, the two-variable symmetric function f(X2)→Y is a complete graph with edges labelled with elements of Y. For multi-variable symmetric functions we have f(Xn)→Y for the complete hypergraph with edges labelled with elements of Y.[10]

Given a discrete-time dynamical system, the trajectories, or orbits (state space) of all the points form a (possibly disconnected) directed graph which is a continuous graph if the system is defined on a continuous space. The trajectories of a continuous-time dynamical system would form a collection of curved paths (phase space) rather than a collection of piece-wise linear paths and so is not a graph in the traditional sense.

Applications

As any graph model, continuous graphs can be used to model many different types of real-world graphs. One arbitrary example is given by peer-to-peer systems.[11]

See also

References

  1. ↑ 1.0 1.1 Webster, J. (1996). "Continuum theory in the digital setting". CiteSeerX: 10.1.1.49.4540.
  2. ↑ Deaconu, Valentin (July 23–26, 1998). "Continuous graphs and C*-algebras". Operator theoretical methods. 17th International Conference on Operator Theory. Timișoara (Romania). ISBN 978-973-99097-2-3. CiteSeerX: 10.1.1.147.1638.
  3. ↑ Geschke, Stefan; Goldstern, Martin; Kojman, Menachem (2004). "Continuous Ramsey Theory on Polish Spaces and covering the plane by functions". Journal of Mathematical Logic. CiteSeerX: 10.1.1.74.6434.
  4. ↑ Geschke, Stefan. "Infinite Ramsey Theory".
  5. ↑ Nahum, Ronny; Zafrany, Samy (1994). "A Topological Linking Theorem in Simple Graphs".
  6. ↑ Nahum, R.; Zafrany, S. (1994). "Topological complexity of graphs and their spanning trees". CiteSeerX: 10.1.1.22.1949.
  7. ↑ Borgs, Christian; Chayes, Jennifer; Lovász, László (2006). "Graph Limits and Parameter Testing". Proceedings of the thirty-eighth annual ACM symposium on Theory of computing. CiteSeerX: 10.1.1.92.2788.
  8. ↑ Lovász, László; Szegedy, Balasz (2006). "Limits of dense graph sequences". J. Combin. Theory Ser. B 96 (6): 933–957. doi:10.1016/j.jctb.2006.05.002.
  9. ↑ Lovász, László; Szegedy, Balasz (2010). "Testing properties of graphs and functions". Israel J. Math. 178: 113–156. doi:10.1007/s11856-010-0060-7.
  10. ↑ Austin, T.; Tao, T. (2010). "Testability and repair of hereditary hypergraph properties". Random Structures and Algorithms. arXiv:0801.2179.
  11. ↑ Naor, M.; Wieder, U. (2007). "Novel architectures for P2P applications: the continuous-discrete approach". ACM Transactions on Algorithms (TALG). CiteSeerX: 10.1.1.64.8030.

Further reading