Continuity set
In measure theory, a continuity set of a measure μ is any Borel set B such that
where 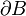 is the boundary set of B. For signed measures, one asks that
is the boundary set of B. For signed measures, one asks that
The class of all continuity sets for given measure μ forms a ring.[1]
Similarly, for a random variable X a set B is called continuity set if
otherwise B is called the discontinuity set. The collection of all discontinuity sets is sparse. In particular, given any collection of sets {Bα} with pairwise disjoint boundaries, all but at most countably many of them will be the continuity sets.[2]
The continuity set C(f) of a function f is the set of points where f is continuous.
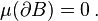
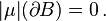
![\Pr[X \in \partial B] = 0,](../I/m/8430dea160eeeb7c68eabf778be7d489.png)