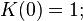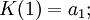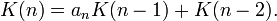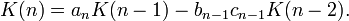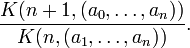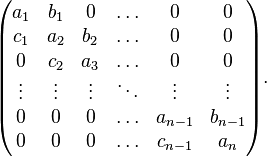Continuant (mathematics)

In algebra, the continuant is a multivariate polynomial representing the determinant of a tridiagonal matrix and having applications in generalized continued fractions.

Definition

The n-th continuant, K(n), of a sequence a = a1,...,an,... is defined recursively by

K(0) = 1 ; \,
K(1) = a_1 ; \,
K(n) = a_n K(n-1) + K(n-2) . \,

It may also be obtained by taking the sum of all possible products of a1,...,an in which any pairs of consecutive terms are deleted.

An extended definition takes the continuant with respect to three sequences a, b and c, so that K(n) is a polynomial of a1,...,an, b1,...,bn−1 and c1,...,cn−1. In this case the recurrence relation becomes

K(0) = 1 ; \,
K(1) = a_1 ; \,
K(n) = a_n K(n-1) - b_{n-1}c_{n-1} K(n-2) . \,

Since br and cr enter into K only as a product brcr there is no loss of generality in assuming that the br are all equal to 1.

Applications

The simple continuant gives the value of a continued fraction of the form [a_0;a_1,a_2,\ldots]. The n-th convergent is

\frac{K(n+1,(a_0,\ldots,a_n))}{K(n,(a_1,\ldots,a_n))} .

The extended continuant is precisely the determinant of the tridiagonal matrix

\begin{pmatrix} a_1 & b_1 & 0 & \ldots & 0 & 0 \\ c_1 & a_2 & b_2 & \ldots & 0 & 0 \\ 0 & c_2 & a_3 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & a_{n-1} & b_{n-1} \\ 0 & 0 & 0 & \ldots & c_{n-1} & a_n \end{pmatrix} .

In Muir's book the "extended" continuant is simply called continuant.

References